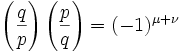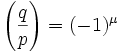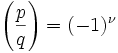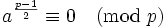In today's blog I continue the
proof for the
Principle of Quadratic Reciprocity. If you are not familiar with the concepts of quadratic reciprocity, quadratic residues, or the Legendre Symbol start
here.
If you would like to start this proof at the beginning, start
here.
If you would like to start with Gauss's Lemma, start
here.
Today's proof is taken from Gareth A. Jones and J. Mary Jones'
Elementary Number Theory.
Lemma 1:if(a) p,q are odd primes(b) P = the set of integers {1, 2, ..., (p-1)/2}(c) N = the set of integers P = { -1, -2, ..., -(p-1)/2 }(d) qx ≡ n (mod p) where n ∈ N, x ∈ Pthen:there exists a y such that (-p/2) is less than (qx - py) which is less than 0.Proof:
(1) There exists
y such that
qx - n = py [Since
qx ≡ n (mod p) -- see
here for review of modular arithmetic]
(2) This then gives us:
qx - py = n.
(3)
qx - py is less than
0 since
n is less than
0.
(4)
qx - py is greater than
(-p/2) since
n ≥ -(p-1)/2 = (-p+1)/2 which is greater than
-p/2.
QED
Lemma 2: if p,q,x,y are integers such that:(a) p,q are positive, odd primes(b) (-p/2) is less than qx - py(c) qx - py is less than 0(d) x,y are positive.Then:(a) there is only 1 value that y can have.(b) 0 is less than qx/p which is less than y(c) y is less than (qx/p) + 1/2.Proof:
(1) Let
y be any integer that satisfies the conditions (a),(b),(c)
(2) There is no value
y' that
y' is an integer and less than
y which satisfies (a),(b),(c) since:
(a)
qx - p(y-1) = qx - py + p(b) We know that
absolute(p) is greater than
absolute(qx-py) since
(-p/2) is less than
(qx-py) which is less than
0.
(c) Since
p is positive and
qx-py is negative, we know that
qx-py + p is greater than
0.
(3) There is no value
y' such that
y' is an integer and greater than
y which satisfies (a),(b),(c) since:
(a)
qx - p(y+1) = qx - py - p(b) Since
-p is greater than
-p/2, we know that
qx-py-p is less than
(-p/2).(4) From (a),(b),(c), we know that
(p/2) is greater than
(py-qx) which is greater than
0.
(5) Dividing (4) by p gives us:
(1/2) is greater than
y - (qx/p) which is greater than
0.
(6) From (5), we know that
y is greater than
(qx/p).
(7) From (5), we also know that
(1/2) + (qx/p) is greater than
y.
(8) Since
q,x,p are positive, we know that
qx/p is greater than
0.
(9) By (#8),(#6), we know that
y is greater than
0.
QED
Lemma 3: if q,p,x,y are integers such that:(a) p,q are positive, odd primes(b) (-p/2) is less than qx - py(c) qx - py is less than 0(d) x ∈ { 1, 2, ..., (p-1)/2 }(e) y is a positive integerThen:y is less than (qx/p) + 1/2 ≤ [q(p-1)]/2p + 1/2 which is less than q+1/2Proof:
(1) From Lemma 2, we know that:
0 is less than
(qx/p) which is less than
y which is less than
(qx/p) + 1/2.
(2) From (d), we know that
x ≤ (p-1)/2.
(3) Combining (1) and (2), we have:
(qx/p) + (1/2) ≤ [q(p-1)]/2p + (1/2)(4) We can conclude that
[q(p-1)]/2p + (1/2) is less than
(q+1)/2 since:
(a)
[q(p-1)]/2p + (1/2) = (qp - q + p)/2p = [(qp/p - q/p + p/p)]/2 == (q - q/p + 1)/2 = (q + 1 - q/p)/2(b)
q/p is greater than
0 since
q,p are odd primes.
(c) From (a) and (b), we have:
(q + 1 - q/p)/2 is less than
(q+1)/2 [ Since
1 - q/p is less than
1 ]
QED
Lemma 4: if q,p are odd primes, then there exist μ, ν where:(a) Using the Legendre Symbol (see here):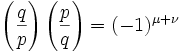 (b) P = set of integer = {1, 2, ... (p-1)/2 }(c) Q = set of integers = {1, 2, ... (q-1)/2 }(d) μ + ν = the number of pairs (x,y) ∈ P x Q such that -p/2 is less than (qx-py) which is less than q/2.
(b) P = set of integer = {1, 2, ... (p-1)/2 }(c) Q = set of integers = {1, 2, ... (q-1)/2 }(d) μ + ν = the number of pairs (x,y) ∈ P x Q such that -p/2 is less than (qx-py) which is less than q/2.Proof:
(1) We can start out with the observation that:
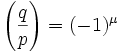
where
μ is the number of pairs
(x,y) ∈ PxQ such that
(-p/2) is less than
qx-py which is less than
0 since:
(a) From Gauss's Lemma (see
here), we have:
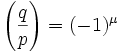
where
μ is the number if elements in
qP ∩ N where
N = of integers
-P, that is,
{-1, -2, ... -(p-1)/2}
(b)
qP ∩ N → qx ≡ n (mod p) where
n ∈ N, x ∈ P. [See
Gauss's lemma for details if needed, see
here for review of modular arithmetic]
(c) There exists
y such that
(-p/2) is less than
qx - py which is less than
0. [By Lemma 1 above]
(d) We know that
y is greater than
0 [See Lemma 2 above]
(e) Also,
y is less than
(q+1)/2. [See Lemma 3 above]
(f) So,
y ≤ (q-1)/2 [ since there is no integer greater than
(q-1)/2 and less than
(q+1)/2 ]
(g) So,
y ∈ Q since (d) gives us
y ≥ 1 and (f) gives us
y ≤ (q-1)/2.
(h) Since
x ∈ P from assumption, we have
(x,y) ∈ PxQ [see
here if you need a review of
PxQ notation]
(2) We can use the same reasoning as (#1) to get a value
ν such that:
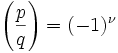
where
ν is the number of pairs
(y,x) ∈ QxP such that
(-q/2) is less than
py-qx which is less than
0 .
(3) Combining (1) and (2) gives us:
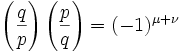
where if
x,y are taken from (#1), we have:
(x,y) ∈ PxQ such that
(-p/2) is less than
qx-py which is less than
0If
x,y are taken from (#2), then we have:
(y,x) ∈ QxP such that
(-q/2) is less than
py-qx which is less than
0(4) Combining both possibilities, we have:
(x,y) ∈ PxQ, (-p/2) is less than
qx-py which is less than
(q/2).
QED