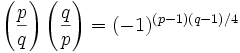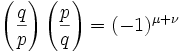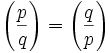Quadratic Reciprocity: Gauss's Lemma for Quadratic Residues

In today's blog I continue the proof for the Principle of Quadratic Reciprocity. If you are not familiar with the concepts of quadratic reciprocity, quadratic residues, or the Legendre Symbol start here.

If you would like to start this proof at the beginning, start here.

Today's proof is taken from Gareth A. Jones and J. Mary Jones' Elementary Number Theory.

Definition 1: Congruence Class (mod n)

The set of all numbers that are congruent to each other modulo a value n. This congruence class is represented in brackets such as [0].

NOTE: If you are not familiar with the concept of congruence or modulo, you can review modular arithmetic here.

If we consider n = 3, then we see that:
[1] = { ... ,-2, 1, 4, 7, ... }

since:

-2 ≡ 4 ≡ 7 ≡ 1 (mod 3).

Definition 2: Unit (mod p)

A congruence class [a] is a unit mod p if there exists another congruence class [b] such that ab ≡1 (mod p).

Here are some examples:

1 is a unit mod 8
3 is a unit mod 8 since (3)(3) ≡ 1 (mod 8)
5 is a unit mod 8 since (5)(5) ≡ 1 (mod 8)
7 is a unit mod 8 since (7)(7) ≡ 1 (mod 8)

Lemma 1: Let p be an odd prime. Let P be the set { 1, 2, ... (p-1)/2 }. Let x,y be elements of P.
Then: x ≠ y → x ± y is not congruent to 0.

(1) Assume that x is less than y (otherwise, we can use the same arguments on y)

(2) Case I: x + y

3 ≤ x + y ≤ (p-1)/2 + (p-1)/2 -1 = (p-1)/2 + (p-1-2)/2 = (2p -4)/2 = p-2.

(3) Case II: x-y

-1 ≥ x-y ≥ 1 - (p-1)/2 = (2 - p + 1)/2 = (-p + 3)/2 = -(p-3)/2

(4) Case III: y-x

1 ≤ y - x ≤ (p-1)/2 - 1 = (p-1-2)/2 = (p-3)/2

QED

Lemma 2: Let p be a prime, let a be an integer such that gcd(a,p)=1. Let P be the set { 1, 2, ... (p-1)/2 }. Then:
x ∈ P, y ∈ P, ax ≡ ± ay → x=y

(1) Assume that ax ≡ ± ay (mod p) and x ≠ y.

(2) ax ± ay ≡ 0 (mod p) [See here for a review of modular arithmetic if needed]

(3) So, p divides a(x ± y)

(4) But p doesn't divide a since gcd(a,p) = 1

(5) So, p divides x ± y [By Euclid's Lemma]

(6) So, x ± y ≡ 0 (mod p)

(7) But x ± y is not congruent to 0 (mod p) from Lemma 1 above.

(8) So we have a contradiction and we reject (#1)

QED

Corollary 2.1: If p is an odd prime and P = { 1, 2, ... (p-1)/2 } and gcd(a,p)=1, then there exists ε_i where aP = { (ε₁₎, (ε₂)(2), ... (ε_(p-1)/2)[(p-1)/2] } and each ε_i = +1 or -1.

(1) We know that each element of aP must be in { ±1, ±2, ... ±(p-1)/2 } since:

(a) Let b be any element of P.

(b) We know that ab must fit into one of the following congruence classes [± 1], [± 2], ... [ ±(p-1)/2 ] since ab (mod p) must be between 0 and p-1.

(c) But this means that either it is between 0 and (p-1)/2 or it is between (p-1)/2 + 1 and p - 1.

(d) If it is between 0 and (p-1)/2 then we are done.

(e) If it is between (p-1)/2 + 1 and p-1, then ab (mod p) is between -(p-1)/2 and -1 since p-1 ≡ -1 (mod p) and since [(p-1)/2 + 1] ≡ -(p-1)/2 (Consider that (p-1)/2 + 1 + (p-1)/2 = (p-1+2 +p - 1)/2 = 2p/2 = p.)

(f) But then either way ab is in { ± 1, ± 2, ... ± (p-1)/2 }

(2) We know that aP = { ±1, ±2, ... ±(p-1)/2 } since:

(a) Let's suppose we have b,c such that b,c ∈ P and b ≠ c.

(b) Then, we know that that ab is not congruent to ac from Lemma 2 since it if they were congruent then they must be the same which contradicts our assumption.

QED

Lemma 3: if p is an odd prime and a is a unit mod p, then a^(p-1)/2 ≡ (∏ε_i) (mod p) where ε_i is derived from aP as in Corollary 2.1 above.

(1) We know that aP = { ± 1, ± 2, ... ±(p-1)/2 } where at each point ε_i = 1 or -1 [See corollary 2.1]

(2) (∏ε_i) ≡ [(a*1)(a*2)...(a*(p-1)/2)]/[(1)(2)...(p-1)/2] (mod p)

NOTE: We can make this assumption since multiplication in modular arithmetic is an abelian group. More details here.

(3) Now, be definition of factorial [(p-1)/2]! ≡ (1)(2)...(p-1)/2 [See here for review of factorials]

(4) Likewise (a*1)(a*2)*...*(a*[p-1]/2) ≡ a^(p-1)/2[(p-1)/2]! (mod p)

(5) Combining #2 with #3 and #4 gives us:
(∏ε_i) ≡ a^(p-1)/2[(p-1)/2]!/[(p-1)/2]! = a^(p-1)/2 (mod p)

QED

Lemma 4: Gauss's Lemma for Quadratic Residues

If p is an odd prime and gcd(q,p)=1, then:



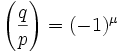
where:
μ = the number of elements in qP ∩ N
P = { 1, 2, ... (p-1)/2 }
N = { -1, -2, ... -(p-1)/2 }

(1) Let x,y be elements of P such that x ≠ y.

(2) qx is not congruent to ± qy (mod p) (from Lemma 2 above)

(3) So, we see from (2) that there are (p-1)/2 distinct congruence classes that are created from qP since for each combination, we know from (2), that there is no overlap.

(4) q^(p-1)/2 ≡ (∏ε_i) (mod p) where ε_i = 1 if (i) ∈ P and ε_i = -1 if (i) ∈ N [From Lemma 3 above]

(5) So, q^(p-1)/2 ≡ (-1)^μ (mod p) where μ = the number of elements in qP ∩ N since:

(a) (∏ε_i) = (-1)^μ where μ is the number of times ε_i = -1. [Since we can ignore all the times ε_i = 1]

(b) But this means we need to figure out the count of all elements b ∈ qP that are also in N.

(c) And this means that we are looking for the number of elements in qP ∩ N.

(6) By Euler's Criterion (see here), we know that:


(7) Combining (5) and (6) gives us our conclusion since the Legendre symbol is only = to 1 or -1.


QED

Quadratic Reciprocity: The Proof

Today, I will present a proof for the Principle of Quadratic Reciprocity:



For those not familiar with quadratic reciprocity, quadratic residues, or with the notation above, start here.

Today's proof is based on the Gareth A. Jones and J. Mary Jones Elementary Number Theory.

Theorem 1: Principle of Quadratic Reciprocity.

Given p,q are odd primes. if p or q ≡ 1 (mod 4), then p is a quadratic residue of q if and only if q is a quadratic residue of p. if both p and q ≡ 3 (mod 4), then p is a quadratic residue of q if and only q is not a quadratic residue of p and likewise, q is a quadratic residue of p if and only if p is not a quadratic residue of q.

(1) Let P be the set of integers {1, 2, ... (p-1)/2 }

(2) Let N be the set of integers -P, that is, {-1, -2, ... -(p-1)/2}

(3) Let Q be the set of integers {1, 2, ... (q-1)/2 }

(4) Now by Gauss's Lemma (see here):



where μ is the number of elements in qP ∩ N. [See here for details on qP ∩ N]

(5) Further, we can conclude (see here):



where μ + ν is the number of pairs (x,y) ∈ PxQ such that -p/2 is less than qx-py is less than q/2.

(6) From a result, I will show later, there exist values α and β such that:

μ + ν = (p-1)(q-1)/4 - (α + β).

(7) Now, it can be shown (see Lemma 2 here), that α = β

(8) With this in place, we combine (#5) with (#6) to get (see Lemma 3 here):



QED

Note: if you are unclear how (#8) is equivalent to the given, see here.

Quadratic reciprocity

Today's blog will focus on the following concepts: quadratic residues, Legendre symbol, and quadratic reciprocity.

The proof for the Rule of Quadratic Reciprocity can be found here.

For details on how quadratic reciprocity relates to the history of Fermat's Last Theorem, see here.

1. Quadratic Residues

The set of quadratic residues is an important concept that derives from modular arithmetic. It is the set of possible congruence values for a given value x². For example, let's look at the quadratic residues for mod 7.

There are 7 possible values for x (mod 7): 0, 1, 2, 3, 4, 5, 6 but we only need to consider the nonzero ones.

To figure out the quadratic residues, we look at the following values:

1² ≡ 1 (mod 7)
2² ≡ 4 (mod 7)
3² ≡ 9 ≡ 2 (mod 7)
4² ≡ 16 ≡ 2 (mod 7)
5² ≡ 25 ≡ 4 (mod 7)
6² ≡ 36 ≡ 1 (mod 7)

So we see that the quadratic residue for 7 consists of { 1, 2, 4}

For purposes of this blog, I will represent the quadratic residue of 7 as Q₇ so that we have:

Q₇ ≡ { 1, 2, 4 }

Since:

1² ≡ 1 (mod 5)
2² ≡ 2 (mod 5)
3² ≡ 4 (mod 5)
4² ≡ 1 (mod 5)

Q₅ ≡ { 1, 2, 4 }

2. Legendre Symbol

The Legendre Symbol is a function that can be defined in terms of quadratic residues. Consider:



This value is defined to equal 0, 1, or -1. In the case above, p is an odd prime and a is any integer. The value is 0 if p divides a. The value is 1 if a is an element of Q_p. The value is -1 if a is not an element of Q_p

We know that Q₇ ≡ { 1, 2, 4}.

If p = 7, a = 14, we know that the value of the Legendre Symbol is 0.

If p = 7, a = 15, we know that the value of the Legendre Symbol is 1 [since 15 ≡ 1 (mod 7)]

If p = 7, a = 17, we know that the value of the Legendre Symbol is -1 [ since 17 ≡ 3 (mod 7)]

3. Quadratic Reciprocity

The idea of quadratic reciprocity builds on top of the Legendre Symbol and refers to the relationship between two odd primes.

In a nutshell, the Rule of Quadratic Reciprocity states the following:



Reviewing exponents, it says that the multiple of two Legendre symbols of two primes is equal to -1 to the power of (p-1)*(q-1)/4. Since p,q are odd primes, p-1 and q-1 are even numbers and their product is divisible by 4.

There are two implications from this.

(1) If p or q ≡ 1 (mod 4), then:



That is, p is a quadratic residue modulo q if and only if q is a quadratic residue modulo p.

This is true since:

(4k+1-1)(4k+1-1)/4 = 16k²/4=4k²=2(2k²)

(4k+1-1)(4k+3-1)/4 = (4k)(4k+2)=(16k² + 8k)/4=4k²+2k =2(2k² + k)

and

(-1)^2k' = 1.

(2) If both p and q ≡ 3 (mod 4), then:



That is, p is a quadratic residue modulo q if and only q is not a quadratic residue modulo p.

This is true since:

(4k+3-1)(4k+3-1)/4 =[16k² + 16k + 4]/4 = 4(k² + k) + 1.

and

(-1)^{4k' + 1} = -1.

This theorem is surprising and nontrivial. Carl Friedrich Gauss considered it one of the most beautiful theorems in all of number theory and worked through 7 different proofs of it. Leonhard Euler first conjectured the theory in 1783. Adrien Legendre provided several attempts at proofs. Still, it was Gauss in 1783 at the age of 18 who provided the first valid proof.

Overview of the background to Kummer's Proof

Ernst Kummer's proof for Fermat's Last Theorem was a major breakthrough in the history of number theory.

To appreciate the importance of Kummer's work with complex numbers, it is valuable to review earlier developments. Kummer came to his discoveries by trying to generalize quadratic reciprocity so it makes sense to review the details behind the basic proof for quadratic reciprocity. Lamé's work used cyclotomic integers which are derived from the roots of unity. For this reason, I will review basic proofs about π and Euler's famous equation: e^iπ = -1.

Kummer's work became the foundation for algebraic number theory. From this view, it makes sense to follow up Kummer's proof with the work of Abel, Galois, as well as the transcendental nature of π.

With this background, it makes sense to go through Dedekind's reinterpretation of Kummer's work which became the foundation of modern algebraic number theory.

Ernst Eduard Kummer

Ernst Eduard Kummer was born in January 29, 1810 in Brandenburg, Prussia. His father was a physician who died when Ernst was 3 years old.

When he was 18, he entered the University of Halle with the intention of becoming a protestant minister. As part of his degree, he was required to take math classes. Over time, he switched his major from theology to mathematics.

In 1831, he won a prize for a mathematical essay that he had written. In honor of this essay, the university awarded him a doctorate in addition to his teaching certificate. That same year, he was teaching mathematics at the Gymnasium.

In 1832, he received a more permanent position at the Gymnasium in Leignitz. There he stayed for 10 years. While there, he taught mathematics and physics. One of his students at this time Leopold Kronecker became a very famous mathematician himself. During this time, Krummer also worked hard on mathematical research and wrote an important paper on hypergeometric series in 1836. From this paper, he began a correspondence with the mathematicians Carl Jacobi and Johann Dirichlet. In 1839, while he was still a school teacher, he was elected to the Berlin Academy of Science.

Life was picking up for Ernst Kummer. In 1840, he married a cousin of Dirichlet and in 1842, he became a full professor at the University of Breslau. Sadly, his wife died in 1848.

In 1855, Kummer became a professor of mathematics at the University of Berlin. He was also able to arrange for his colleagues Karl Weierstrass and Leopold Kronecker to also get positions at the University of Berlin. From this point, Berlin became one of the leading mathematical centers of all Europe.

Kummer made major contributions to function theory and number theory. In function theory he extended Gauss's work on hypergeometric series. In number theory, he proposed the concept of "ideal" numbers which later led to the theory of rings which is the foundation of modern algebraic number theory. His work on number theory also led to a major breakthrough on Fermat's Last Theorem.

For his work on Fermat's Last Theorem, Kummer won the Grand Prize from the Paris Academy of Sciences in 1857. He was later elected to the Paris Academy of Science and the Royal Society of London in 1863.

Kummer died on May 14, 1893 when he was 83.

References

• MacTutor biography of Ernst Kummer
  

Lamé's Proposed Proof

On March 1, 1847, Gabriel Lamé announced that he believed that he had found a full proof for Fermat's Last Theorem. He presented to the Paris Academy the outline of what he believed was a complete proof. Earlier he had succeeded in the first proof for x⁷ + y⁷ = z⁷.

The approach that he offered involved what are known as the Roots of Unity. This involves complex numbers such as α where:

αⁿ = 1 and α ≠ ± 1.

The proof is based on the following equation:

xⁿ + yⁿ = (x + y)(x + αy)(x + α²y) .... (x + α^n-1y)

The essence of the proof is showing that each of the x+α^ey is relatively prime to the others so that it represents an nth power (since they are all equal to zⁿ). Then, one shows how this condition leads to infinite descent.

Lamé claimed that this work was largely based on the work done by Joseph Liouville.

Liouville was present at the Paris Academy at this time and spoke after Lamé. He was not as confident as Lamé about the success of the proof. In fact, he suggested that Lamé approach was rather obvious and would have occurred to anyone who had worked long enough with complex numbers.

Liouville claimed that Lamé's assumption about unique factorization of the roots of unity was not necessarily justified and absent unique factorization, the proof was not valid.

The next person to speak was Augustin Cauchy. Cauchy was more optimistic about the possibilities of Lamé's approach. He announced that he too was very close to a solution to Fermat's Last Theorem using a similar technique.

On March 15, Pierre Wantzel announced that he had a proof about the unique factorization of the roots of unity. His proof showed unique factorization for the case where n = 2 and n=3. He then claimed that "one easily sees" the validity for cases where n ≥ 4. In a short time, Cauchy came back demonstrating that Wantzel's method did not work for n ≥ 4.

At this point, a competition broke out between Lamé and Cauchy to prove unique factorization for n ≥ 4. On March 22, both men deposited "secret packets" to the Paris Academy, a method that was used to establish priority.

Unfortunately, as is usually the case, the devil is in the details and the proof for unique factorization turned out to be more complicated than Lamé and Cauchy had forseen. In May 24, Liouville announced a proof by Ernst Kummer that settled the question by demonstrating that Lamé's complex numbers lacked unique factorization. In fact, Kummer had first presented this proof in a mathematical journal three years earlier.

But there was hope. Kummer's conclusion was that unique factorization could be "saved" by using "ideal complex numbers." Kummer's ideal complex numbers would turn out to be a major breakthrough in the generalization of Fermat's Last Theorem. It would also turn out to be the foundation for what is today known as algebraic number theory.

Today's blog was taken from Harold M. Edwards' Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory. (All quotes come from Edwards' original text).

So ends Phase I of the History of Fermat's Last Theorem

With yesterday's posting, I have completed Phase I of the history of Fermat's Last Theorem.

The original goal of this blog was to divide up the history into three phases:

Phase I: Early Achievements

Phase II: Kummer's Achievement

Phase III: Wile's Achievement

As part of the first phase, I have done blogs on the following mathematicians:

• Johann Dirichlet
  
• Diophantus of Alexandria
• Ferdinand Eisenstein
  
• Leonhard Euler
  
• Pierre de Fermat
• Carl Friedrich Gauss
• Sophie Germain
• Joseph Lagrange
  
• Gabriel Lamé
• Adrien Legendre
• Sir Isaac Newton
  
• Blaise Pascal

It was very fun to revisit the early proofs and I was very surprised at the response that I received. To date, this blog has been growing by 10-20% each month since April of last year. This month, this blog will have over 2500 unique visitors.

Thanks to everyone who has provided questions and comments on the different parts of each proof. Please continue to point out areas which are unclear or details which can be improved.

Thanks to everyone for your support. I am very glad (and surprised) to see that there is a growing audience for number theory and for a blog that is not much more than the details behind famous mathematical proofs.

Cheers,

-Larry

Fermat's Last Theorem: Proof for n=7: v cannot be even

In today's blog, I will continue the proof for Fermat's Last Theorem n=7.

The details for today are based on Paulo Ribenboim's Fermat's Last Theorem for Amateurs.

Lemma 1: if :
(a) 2 * 7^4e-1 *A⁴= s² + 3 * 7^2ev² ± u
(b) 2 * B⁴ = s² + 3 * 7^2ev² ± u
(c) s, A, B, v are an integers
(d) gcd(A,B) = 1
(e) v is even
(f) s is odd
Then
B is not even

Proof:

(1) Assume B is even

(2) Then A is odd

(3) Adding the two values together gives us:
( s² + 3 * 7^2ev² ± u) + ( s² + 3 * 7^2ev² ± u) = 2s² + 2*3*7^2ev² = 2 * 7^4e-1 *A⁴ + 2 * B⁴

(4) Dividing both sides by 2 gives us:
s² + 3*7^2ev² = 7^4e-1 * A⁴ + B⁴

(5) Subtracting 3*7^2ev² from both sides gives us:
s² = -3*7^2ev² + 7^4e-1*A⁴ + B⁴

(6) But from #5 and from a previous result (see here), we get:
s² ≡ (-3)(1)(v²) + (-1)^4e-1(1) + (B²)² (mod 8)

(7) Also, from a previous result (see here), we know that B² ≡ 0 or 4 (mod 8).

(8) So that (B²)² ≡ 0 (mod 8) since:

(a) (0)² ≡ 0 (mod 8)

(b) (4)² ≡ 16 ≡ 0 (mod 8)

(9) So applying (#9) to (#7) gives us:
s² ≡ (-3)v² + (-1)^4e-1(1) + (0) ≡ (-3)v² - 1.

(10) But since v is even, there exists v' such that v = 2v' and this means that:
v² ≡ (2v')² ≡ 4v'² ≡ 0 since:

(a) So, v'² ≡ 0 or 4 (mod 8)

(b) (4)(0) ≡ 0 (mod 8)

(c) (4)(4) ≡ 16 ≡ 0 (mod 8)

(11) Combining (#11) with (#10) gives us that:
s² ≡ -1 (mod 8).

(12) But this is impossible since s² ≡ 1 (mod 8) by a previous result (see here)

(13) So we have a contradiction and we reject our assumption.

QED

Lemma 2: if:
(a) 2 * 7^4e-1 *A⁴= s² + 3 * 7^2ev² ± u
(b) 2 * B⁴ = s² + 3 * 7^2ev² ± u
(c) s, A, B, v are an integers
(d) gcd(A,B) = 1
(e) v is even
(f) s is odd
(g) A is even
Then
There exists an integer A'' such that A = 8A''

Proof:

(1) B is odd [since A is even and gcd(A,B)=1]

(2) Since A is even, there exists a value A' such that A= 2A'

(3) Since s is odd and from a previous result (see here), we have:
s² ≡ 1 (mod 8)

(4) Adding (a) and (b), we get:
2*s² = -3 *2* 7^2ev² + 2*7^4e-1A⁴ + 2*B⁴

(5) Since 2v=AB, we can also write:
s² = -3 * 7^2e([1/2]AB)² + 7^4e-1A⁴ + B⁴ =
= -3*7^2e(A'B)² + 7^4e-1A⁴ + B⁴

(6) From (#5) and a previous result (see here):
s² ≡ (-3)(1)(A')²(1) + (-1)^4e-1(0) + (1) ≡
≡ (-3)(A')² + 1 (mod 8)

(7) Combining (#6) with (#3) gives us:
s² ≡ (-3)(A') + 1 ≡ 1 (mod 8)

(8) This implies:
(-3)(A')² ≡ 0 (mod 8)

(9) Which mean that A' must be divisible by 4 since:

(-3)(0)² ≡ 0 (mod 8)
(-3)(1)² ≡ -3 (mod 8) which doesn't work.
(-3)(2)² ≡ (-3)(4) ≡ -4 (mod 8) which doesn't work
(-3)(3)² ≡ (-3)(9) ≡ -27 ≡ -3 (mod 8) which doesn't work
(-3)(4)² ≡ (-3)(16) ≡ -48 ≡ 0 (mod 8)
(-3)(5)² ≡ (-3)(25) ≡ -75 ≡ -3 (mod 8) which doesn't work
(-3)(6)² ≡ (-3)(36) ≡ -108 ≡ -4 (mod 8) which doesn't work
(-3)(7)² ≡ (-3)(49) ≡ -147 ≡ -3 (mod 8) which doesn't work

(10) So there exists A'' such that A' = 4A'' = 8A

QED

Lemma 3: if :
(a) 2 * 7^4e-1 *A⁴= s² + 3 * 7^2ev² ± u
(b) 2 * B⁴ = s² + 3 * 7^2ev² ± u
(c) s, A, B, v are an integers
(d) gcd(A,B) = 1
(e) v is even
(f) s is odd
(g) A is even
Then
There exists A'' such that A=8A'' and:
(s - B² + 3*8*7^2eA''²)(s + B² - 3*8*7^2eA''²) = 7^4e-1*4*(2A'')⁴

Proof:

(1) From Lemma 2 above, we know that there exists A'' such that A=8A''.

(2) Adding (a) and (b) together gives us:
s² = -3 * 7^2e([1/2]AB)² + 7^4e-1A⁴ + B⁴ =
= -3*7^2e(A'B)² + 7^4e-1A⁴ + B⁴

(3) -3*16*7^2e(A'')²B² + 7^4e-1*8⁴*(A'')⁴ + B⁴

(4) Now,
(B² - 3*8*7^2e(A'')²)² = B⁴ - 2*3*8*7^2e(A'')²B² + 9*64*7^4e(A'')⁴

(5) So,
s² - (B² - 3*8*7^2e(A'')²)² = 7^4e-1*8⁴*(A'')⁴ - 3²*8²*7^4e(A'')⁴ =
= 7^4e-1(8⁴*(A'')⁴ - 3²*8²*7(A'')⁴) =
= 7^4e-1*8²(8²(A'')⁴ - 3²*7(A'')²) =
= 7^4e-1*8²(64(A'')⁴ - 63(A'')⁴) =
= 7^4e-1*8²(A'')⁴

(6) Putting it altogether gives us:
(S - B² + 3*8*7^2e(A'')²)(S + B² + 3*8*7^2e(A'')²) = 7^4e-1*8²*(A'')⁴ =
= 7^4e-1*4*(2A'')⁴

QED

Lemma 4: x² ≡ 0, 1, 2, or 4 (mod 7)

Proof:

(0)² ≡ 0 (mod 7)
(1)² ≡ 1 (mod 7)
(2)² ≡ 4 (mod 7)
(3)² ≡ 9 ≡ 2 (mod 7)
(4)² ≡ 16 ≡ 2 (mod 7)
(5)² ≡ 25 ≡ 4 (mod 7)
(6)² ≡ 36 ≡ 1 (mod 7)

QED

Lemma 5: if :
(a) 2 * 7^4e-1 *A⁴= s² + 3 * 7^2ev² ± u
(b) 2 * B⁴ = s² + 3 * 7^2ev² ± u
(c) s, A, B, v are an integers
(d) gcd(A,B) = 1
(e) v is even
(f) s is odd
(g) A is even
Then
There exists A'' such that A=8A'' and:
(s - B² + 3*8*7^2eA''²)(s + B² - 3*8*7^2eA''²) ≠ 7^4e-1*4*(2A'')⁴

Proof:

(1) Assume that (s - B² + 3*8*7^2eA''²)(s + B² - 3*8*7^2eA''²) = 7^4e-1*4*(2A'')⁴.

(2) Both (s - B² + 3*8*7^2eA''²) and (s + B² + 3*8*7^2eA''²) are even since:

(a) s is odd, B is odd (since A is even and gcd(A,B)=1.)

(b) odd - odd + even = even

(c) odd + odd + even = even

(3) gcd(s - B² + 3*8*7^2eA''² , s + B² - 3*8*7^2eA''²) = 2 since:

(a) Let p be a prime that divides both and which does not equal 2.

(b) Since p divides both it also divides (s - B² + 3*8*7^2eA''² ) + (s + B² + 3*8*7^2eA''²) = 2s.

(c) Since p is odd, it divides s.

(d) By assumption p must divide 7^4e-1*4*(2A'')⁴.

(e) But this means p must divide 7^4e-1 or A''.

(f) p ≠ 7 since it divides s and s is not divisible by 7.

(g) p cannot divide A'' since by S - B² + 3*8*7^2eA''², it would have to divide B but this is impossible since gcd(A,B)=1.

(h) So we have a contradiction and decide that p=2.

(i) Let f be the gcd. By (h), it must be a power of 2.

(j) By the logic in (b), it must divide 2s which means that it must = 2 since s is odd.

(4) From (#1), we can conclude that:

(a) 7^4e-1 divides 1 of the two multiples.

(b) We know that there exists c,d such that cd=2A'' and c⁴ divides 1 of the multiplies and d⁴ divides the other and gcd(c⁴,d⁴) = 1.

(c) So, we can assume that:
s ± B² ± 3*8*7^2eA''² = 2c⁴

s ± B² ± 3*8*7^2eA''² = 7^4e-12d⁴

(5) Subtracting these two equations so that we remove the s gives us:
± 2B² = ±6*8*7^2eA''² - 2c⁴ + 7^4e-12d⁴

(6) Dividing both sides by 2 gives us:
± B² = ± 6*4*7^2eA''² - c⁴ + 7^4e-1d⁴ =
= ± 6*7^2e(2A'')² - c⁴ + 7^4e-1d⁴ =
= ± 6*7^2ec²d² - c⁴ + 7^4e-1d⁴

(7) We know that 7 does not divide B

If 7 divided B, then 7 would divide c from (#6), and then it would divide s from (#4c) which is impossible since s is not divisible by 7.

(8) And we also know that 7 does not divide c.

If 7 divided c, then 7 would divide B from (#6) and the same argument applies.

(9) So ± B² + c⁴ ≡ 0 (mod 7) from (#6)

(10) But then we have ± B² + (1, 2, or 4) which means ± must actually be "-".

(11) This then gives us: -B² = -6*7^2ec²d² -c⁴ + 7^4e-1d⁴

(12) Multiplying -1 to each side gives us:
B² = c² + 6*7^2ec²d² - 7^4e-1d⁴

(13) But this equation leads to an infinite descent by a previous lemma (see step #5 in Lemma 1 here) since:

v = AB/2 = 4A''B ≥ 2cd which is greater than d.

(14) So we reject our assumption at (1).

QED

Lemma 6: If there exists s,u,v such that:
(a) (s² + 3 * 7^2ev² + u)(s² + 3 *7^2ev - u) = 64 * 7^4e-1v⁴
(b) gcd(s² + 3 * 7^2ev² + u , s² + 3 *7^2ev - u) = 2ⁿ where n ≥ 0.
(c) 7 doesn't divide s
(d) t = 7^ev
(e) gcd(t,s)=1
Then
v is not even.

Proof:

(1) Assume that v is even.

(2) Then t must be even and s must be odd from (d) and (e).

(3) u must also be odd since:

(a) Assume u is even.

(b) (s² + 3 * 7^2ev² + u)(s² + 3 *7^2ev - u) = 64 * 7^4e-1v⁴

(c) (odd² + odd*odd*even + even)(odd² + odd*odd*even - even) =
(odd + even + even)(odd + even - even) = (odd)(odd) = odd

(d) Which contradicts (b) so we reject our assumption (a).

(4) Since v is even, we know that there exists v' such that:
v = 2v'

(5) Since u is odd, we know that both (s² + 3 * 7^2ev² + u) and (s² + 3 *7^2ev - u) are even since:

odd*odd + odd*odd*even*even + odd = odd + even + odd = even.

(6) This gives us the following:
(s² + 3 * 7^2ev² + u)(s² + 3 *7^2ev - u) = (2)(2) * 7^4e-1(16)v⁴

(7) From (b) above we know that 7^4e-1 divides either one or the other since if it did not divide only 1, there would a common factor of 7 which is not the case.

(8) From (#6) and (#7), we can posit that there exists A,B such that:
AB = 2v

And (2v)⁴ = A⁴B⁴

(9) And putting this into (6) gives us:
(s² + 3 * 7^2ev² + u)(s² + 3 *7^2ev - u) = (2)(2) * 7^4e-1(16)v⁴ = (2)(2)* 7^4e-1A⁴B⁴

Where:

2*7^4e-1A⁴ divides either (s² + 3 * 7^2ev² + u) or (s² + 3 *7^2ev - u) and
2*B⁴ divides the other one.

(10) We note further that gcd( s² + 3 * 7^2ev² + u, s² + 3 *7^2ev - u) can be at most 2 since:

(a) Let f = the greatest common denominator.

(b) f must divide (s² + 3 * 7^2ev² + u) - (s² + 3 *7^2ev - u) = 2u

(c) We know from our assumption that f must be a power of 2.

(d) We also know that u is odd.

(e) This means that f must = 2.

(11) So, we have the following:

(a) s² + 3 * 7^2ev² ± u = 2 * 7^4e-1A⁴

(b) s² + 3 * 7^2ev² ± u = 2 * B⁴

(c) we can further conclude that gcd(A,B) = 1 since:

If an odd prime divides gcd(A,B), then this same odd prime would divide (s² + 3 * 7^2ev² + u) and (s² + 3 *7^2ev - u) which goes against our assumption.

If 2 divides gcd(A,B), then then we would have 4 would divide both but this impossible since the gcd can be at most 2.

(d) There are two possible cases to consider:

(i) A is odd, B is even
(ii) A is even, B is odd

We know that they cannot both be even from (#11c). We know that one must be even since they are equal to 2v (#8)

(12) B is not even (see Lemma 1 above)

(13) So A is even.

(14) So (s - B² + 3*8*7^2eA''²)(s + B² - 3*8*7^2eA''²) = 7^4e-1*4*(2A'')⁴ [From Lemma 3 above]

(15) But simultaneously, from Lemma 5 above we have:
(s - B² + 3*8*7^2eA''²)(s + B² - 3*8*7^2eA''²) ≠ 7^4e-1*4*(2A'')⁴

(16) So we have a contradiction and we reject (#1).

QED

Fermat's Last Theorem: Proof for n=7: v cannot be odd

In today's blog, I will continue the proof for Fermat's Last Theorem n=7.

The details for today are based on Paulo Ribenboim's Fermat's Last Theorem for Amateurs.

Lemma 1: if x is odd, then x² ≡ 1 (mod 8).

(1) Since x is odd, there exists a value x' such that x = 2x' + 1.

(2) x² = (2x' + 1)² = 4x'² + 4x' + 1 = 4(x'² + x') + 1

(3) Now x'² + x' is even since:

Case I: x' is odd

odd + odd² = odd + odd = even.

Case II: x' is even

even + even² = even + even = even

(4) So, we can suppose that there exists x'' such that x'² + x' = 2x''

(5) Which gives us 4(2x'') + 1 = 8x'' + 1

QED

Lemma 2: if x is even, then x² ≡ 0 or 4 (mod 8)

(1) From modular arithmetic, we only need to show this is true where x = 0, 2, 4, or 6 since any other even number will equate to these results. (See here for review of modular arithmetic)

(2) Now, we try out the 4 possible even values:

(0)² ≡ 0 (mod 8)
(2)² ≡ 4 (mod 8)
(4)² ≡ 16 ≡ 0 (mod 8)
(6)² ≡ 36 ≡ 4 (mod 8)

QED

Lemma 3: if:
(a) (s² + 3 * 7^2ev² + u)(s² + 3 *7^2ev - u) = 64 * 7^4e-1v⁴
(b) gcd(s² + 3 * 7^2ev² + u , s² + 3 *7^2ev - u) = 2ⁿ where n ≥ 0.
(c) v is odd
Then there exists a,b such that:
(a) (8s + 32b² - 3 *7^2ea²)(8s - 32b² + 3* 7^2ea²) = 7^4e-1a⁴
(b) a,b are odd
(c) gcd(a,b)=1

Proof:

(1) From (b), we know that 7^4e-1 divides either (s² + 3 * 7^2ev² + u) or (s² + 3 *7^2ev - u) [Otherwise, 7 could be a common factor which is not the case.

(2) We can suppose two values A,B such that AB=64 and A divides the same value as (1) while B divides the other one.

(3) Also, we can suppose two values a,b such that v = ab where a divides the same value as (1) while b divides the other.

(4) We know that a,b are odd since v is odd and odd = odd * odd.

(5) We also know that gcd(a,b)=1 from (b). If this wasn't the case, then there would be an odd prime that was a common factor which (b) tells us is not the case.

(6) Putting this altogether, we get:
(a) s² + 3 * 7^2ea²b² ± u = 7^4e-1Aa⁴
(b) s² + 3 * 7^2ea²b² ± u = Bb⁴

NOTE: I used ± since we don't which one is (a) and which one is (b). The important point is that they complementary so if (a) were "+", then b would be "-".

(7) Adding (a) and (b) together gives us:
2s² + 6 * 7^2ea²b² = 7^4e-1Aa⁴ + Bb⁴

NOTE: Because (a) and (b) are complementary, the u cancels out.

(8) From #7, we get:
2s² = -6 * 7^2ea²b² + 7^4e-1Aa⁴ + Bb⁴

(9) So that:
s² = -3 * 7^2ea²b² + 7^4e-1(A/2)a⁴ + (B/2)b⁴

(10) Since s is an integer, we know that A/2 and B/2 must be integers.

(11) So we can deduce from (9)

s² ≡ -3(7^2e)a²b² + 7^4e-1(A/2)a⁴ + (B/2)b⁴ (mod 8)

(12) Applying Lemma 1 and the fact that a,b are odd gives us:

s² ≡ (-3)(1)(1)(1) + (-1)^4e-1(A/2)(1) + (B/2)(1) ≡

≡ (-3) + (-1)(A/2) + (B/2) ≡ -3 - (A/2) + (B/2) (mod 8)

(13) Now from (#12), (#2), and (#10) we can deduce that A = 2, B = 32 since:

The possible values for A,B are (2,32), (4,16), (8, 8), (16,4), (32,2)

If S is odd, then S² ≡ 1 (mod 8) from Lemma 1.
If S is even, then S² ≡ 0 or 4(mod 8) from Lemma 2.

So, now we show that of the 5 possible values for A,B only (2,32) works:

Case I: A=2, B = 32 is possible since:

-3 -(A/2) + (B/2) ≡ -3 -(2/2) + (32/2) ≡ -3 - 1 + 16 ≡ 20 ≡ 4 (mod 8)

Case II: A=4, B=16 is impossible since:

-3-(A/2) + (B/2) ≡ -3 -(4/2) + (16/2) ≡ -3 -2 + 8 ≡ 3 (mod 8)

Case III: A=8, B=8 is impossible since:

-3-(A/2) + (B/2) ≡ -3 - (8/2) + (8/2) ≡ -3 -4 + 4 ≡ -3 (mod 8)

Case IV: A=16, B = 4 is impossible since:

-3-(16/2) + (4/2) ≡ -3 -8 + 2 ≡ -9 ≡ -1 (mod 8)

Case V: A=32, B = 2 is impossible since:

-3 - (32/2) + (2/2) ≡ -3 -16 + 1 ≡ -18 ≡ -2 (mod 8)

(14) So using (#13) with (#19), we get:

s² = -3 * 7^2ea²b² + 7^4e-1(A/2)a⁴ + (B/2)b⁴ =
= -3 * 7^2ea²b² + 7^4e-1(2/2)a⁴ + (32/2)b⁴ =
= -3 * 7^2ea²b² + 7^4e-1a⁴ + 16b4.

(15) This can be adjusted to:
s² + 3 * 7^2ea²b² = 7^4e-1a⁴ + 16b⁴

(16) Multiplying both sides by 64 gives us:
64² + 6 * 7^2e*32a²b² = 7^4e-1*64a⁴ + 64*16b⁴

(17) Subtracting 64*16b⁴ from both sides gives us:
64s² + 6 * 7^2e * 32a²b² - 64 * 16b⁴ = 7^4e-1*64a⁴

(18) Since (32b² - 3 * 7^2ea²)² = 64*16b⁴ - 6*7^2e32a²b² + 3²*7^4ea⁴, we can change (#17) into:

64s² - (32b² - 3*7^2ea²)² =
= 7^4e-1 * 64a⁴ -3²7^4ea⁴ = (64 - 9*7)7^4e-1a⁴ = 7^4e-1a⁴

(19) But then we have:

(8s + (32b² - 3*7^2ea²)(8s - 32b² - 3*7^2ea²) =
= (8s + 32b² - 3*7^2ea²)(8s - 32b² + 3*7^2ea2) = 7^4e-1a⁴

QED

Lemma 4: if (8s + 32b² - 3 *7^2ea²)(8s - 32b² + 3* 7^2ea²) = 7^4e-1a⁴
with a,b are odd, gcd(a,b)=1, and 7 doesn't divide s then gcd(8s + 32b² - 3 *7^2ea², 8s - 32b² + 3* 7^2ea²) = 1.

(1) Assume that the gcd(8s + 32b² - 3 *7^2ea², 8s - 32b² + 3* 7^2ea²) is greater than 1.

(2) Then there exists a prime p that divides both.

(3) Adding the two values together, we get that p divides 16s which means that p divides 16 or p divides s by Euclid's Lemma.

(4) First, we note that p ≠ 2 since:

(a) s is either even or odd.

(b) if s is even, then 8s ± 32b² ±3*7^2ea² =
= (even)(even) ± (even)(odd)² ±(odd)*(odd)^2e(odd)² =
= (even) ± (even) ± (odd) = odd.

(c) Likewise, if s is odd, then then 8s ± 32b² ±3*7^2ea² =
= (even)(odd) ± (even)(odd)² ±3*7^2ea² =
= (even) ± (even) ± (odd) = odd.

(5) This means that p must divide s.

(6) By our original assumption p must divide 7^4e-1a4.

(7) But since p divides s, we know that p ≠ 7 since 7 doesn't divide s.

(8) This means that p must divide a again by Euclid's Lemma.

(7) But combining (#5) and (#2) gives us that p must divide 32b² - 3*7^2ea²

(8) Which would mean since p divides a and p ≠ 2, then p must divide b² which means that p divides b.

(9) But this is impossible since gcd(a,b) = 1.

QED

Lemma 5: If there exists s,u,v such that:
(a) (s² + 3 * 7^2ev² + u)(s² + 3 *7^2ev - u) = 64 * 7^4e-1v⁴
(b) gcd(s² + 3 * 7^2ev² + u , s² + 3 *7^2ev - u) = 2ⁿ where n ≥ 0.
(c) 7 doesn't divide s
Then
v is not odd.

Proof:

(1) Assume that v is odd.

(2) From Lemma 3, we know that there exists a,b such that:
(8s + 32b² - 3 *7^2ea²)(8s - 32b² + 3* 7^2ea²) = 7^4e-1a⁴
a,b are odd
gcd(a,b)=1

(3) From Lemma 4, we know that:
gcd(8s + 32b² - 3 *7^2ea², 8s - 32b² + 3* 7^2ea²) = 1.

(4) From this, we know that 7^4e-1 divides either 8s + 32b² - 3 *7^2ea² or 8s - 32b² + 3* 7^2ea².

(5) Also, we know that there must exist two odd integers c,d such that:
(a) a = cd
(b) 7^4e-1c⁴ divides either 8s + 32b² - 3 *7^2ea² or 8s - 32b² + 3* 7^2ea² while d⁴ divides the other one.

(6) From #3, we know that gcd(c,d)=1 [otherwise we violate step (#3).]

(7) Adding the two values in (#4) together gives us:
d⁴ ≡ 8s ± 32b² ± 3*7^2ea² ≡ (0) ± (0) & #177; 3 * 7^2ea² ≡ ±3 * 7^2ea² (mod 8)

(8) From Lemma 1, since 7^2e = (7^e)² and since a is odd, this gives us:
d⁴ ≡ ±(3)(1)(1) ≡ ± 3 (mod 8)

(9) But this is impossible since d is odd, d² is odd and (odd)² ≡ 1 (mod 8) from Lemma 1.

(10) Therefore we have a contradiction and we reject our assumption.

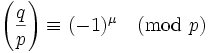
QED