Today's blog continues the discussion on Pell's Equation. For those interested in the background of this problem, start here. For those interested in understanding how this relates to Fermat's Last Theorem, start here.
In a previous blog, I explained how continued fractions can be used to solve Pell's Equation. In today's blog, I will go into more detail about a method for determining the representation of a continued fraction. This method is assumed in the solution to Pell's Equation which is found here.
Today's blog is based on the Jody Esmonde and M. Ram Murty's Problems in Algebraic Number Theory.
Theorem: For any irrational number α, it is possible to represent it in the form
[ a0, a1, ... ] where all values ai are integers and where we use the following equations:
(a) α0 = α
(b) ak = floor(αk)
(c) αk+1 = 1 / (αk - ak)
(1) First, I show this is true for the case k = 0.
α = α0 = floor(α0) + [α0 - floor(α0)] =
= a0 + 1/α1
(2) Assume it is true up to [a0, ..., αk]
(3) We see that:
αk = floor(αk) + [αk - floor(αk] =
= ak + 1/αk+1 =
[ a0, ..., ak, αk+1]
(4) By the Principle of Induction (see here), we are done.
QED
To show how this method can be used, let's apply it some examples:
Example 1: √6
a0 = floor(√6) = 2.
α1 = 1 / (√6 - 2) =
= (√6 + 2)/(6 - 4) =
= (√6 + 2)/2
a1 = floor([√6 + 2]/2) = 2
α2 = 1/[(√6 + 2)/2 - 2] =
= 1/[(√6 + 2 - 4)/2] =
= 1/[(√6 - 2)/2] =
= 2/(√6 - 2) =
= 2(√6 + 2)/(6 - 4) = 2(√6 + 2)/2 =
= √6 + 2
a2 = floor(√6 + 2) = 4.
α3 = 1/(√6 + 2 - 4) =
= 1/(√6 - 2) =
= (√6 + 2)/2
Since, this is the same as α1 so we have reached a repetition and we are done.
√6 = [ 2, 2, 4 ]
We note that:
n = 1 [Position where repetition begins is a1]
p = 2 [Size of period. The representation repeats every two items]
Example 2: √23
a0 = floor(√23) = 4.
α1 = 1/(√23 - 4) =
= (√23 + 4)/(23 - 16) =
= (√23 + 4)/7
a1 = floor([√23 + 4]/7) = 1
α2 = 1/[ (√23 + 4)/7 - 1] =
= 1/[(√23 + 4 - 7)/7] = 1/[(√23 -3)/7] = 7/(√23 -3) =
= 7(√23 +3)/(23 - 9) = 7(√23 +3)/14 = (√23 +3)/2
a2 = floor([√23 +3]/2 ) = 3.
α3 = 1/[(√23 +3)/2 - 3] = 1/[(√23 +3 - 6)/2 ] = 1/[(√23 - 3)/2 ] =
= 2/(√23 - 3) = 2(√23 + 3)/(23 - 9) =
= (√23 + 3)/7
a3 = floor([√23 + 3]/7) = 1.
α4 = 1/[(√23 + 3)/7 - 1] = 1/[(√23 + 3 - 7)/7 ] =
= 1/[(√23 - 4)/7 ] = 7/(√23 - 4) = 7(√23 + 4)/(23-16) =
= √23 + 4
a4 = floor(√23 + 4) = 8.
α5 = 1/(√23 + 4 - 8) = 1/(√23 - 4)
This turns out to be the same value as α1 so we are done.
√23 = [ 4, 1, 3, 1, 8 ]
We note that:
n = 1 [Position where repetition begins is a1]
p = 4 [Size of period. The representation repeats every four items]
Saturday, December 31, 2005
Sunday, December 18, 2005
Continued Fractions and Matrices
Matrices are very useful when analyzing continued fractions. In previous blogs, I wrote about the continued fractions approximation function and the continued fractions basic properties. Today, I will show how matrices can be used to reason with continued fractions.
Today's blog is based on H. M. Stark's An Introduction to Number Theory. If you are not familiar with Continued Fractions, start here. If you are not familiar with the Continued Fraction approximation algorithm, start here.
A continued fraction breaks a real number into a series of integers such as a0, a1, ... an. It makes sense that we can use matrices to reason about them.
In today's blog, I will focus on the simplest properties of matrices. For example, I will only deal with two types of matrices:
1 x 2 matrices such as (5,6)
2 x 2 matrices
For those who would need a review of simple matrices, matrix products, determinants, inverses, or some basic lemmas, start here.
To represent, continued fractions as matrices, we define the following:
(a) An
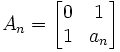
NOTE: an is taken directly from the continued fraction. See here for details on how this is generated.
(b) Mn
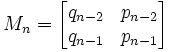
NOTE: pn, qn are generated based on the continued fraction approximation function. See here for details on how these two values are generated.
(c) γn
γn = qn-2 + αnqn-1
NOTE: αn is generated based on the continued fraction for α (see here). qn is generated based on the continued fraction approximation algorithm (see here).
Using these definitions, I will go through some lemmas that will be useful in solving Pell's equation.
Lemma 1: Mn+1 = AnMn
(1) AnMn =
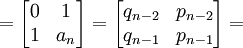
NOTE: By the definitions above.
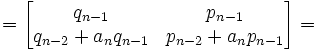
NOTE: By carrying out the matrix product [see here for review if needed]
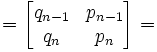
NOTE: By applying the definitions of pn and qn [see here for details]
= Mn+1 [By the definition above]
QED
Lemma 2: γn(1,α) = (1,αn)Mn
(1) (1,αn)Mn =
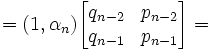
= (qn-2 + αnqn-1 , pn-2 + αnpn-1) [See here to review matrix products]
= (qn-2 + αnqn-1)(1,α) [Since α * (qn-2 + αnqn-1) = pn-2 + αnpn-1; see here]
= γn(1,α)
QED
Lemma 3: α is irrational → γn ≠ 0
(1) Since α is irrational, αn is irrational. (See here for proof; only rational numbers give way to rational αn)
(2) Assume γn = 0.
(3) Then, qn-2 + αnqn-1 = 0.
(4) Then qn-2=0 and qn-1 = 0. [See here for proof]
(5) q-1 = q1 - q0a1 = a1 - a1(1) = 0
q-2 = q0 - q-1a0 = 1 - 0*a0 = 1
NOTE: See here for review of qn
(6) We also know for all values n ≥ 1, that qn ≥ 1 (see here).
(7) So (#4) is impossible and we reject our assumption.
QED
Lemma 4: det(Mn) = (-1)n
(1) det(Mn) = pn-1qn-2 - pn-2qn-1 (See here for a review of determinants)
(2) So, det(Mn) = (-1)n by a previous result. (See here)
QED
Lemma 5: Mn+1 = AnAn-1...A1A0
(1) Mn+1 = AnMn (From Lemma 1 above)
(2) Applying Lemma 1 again gives us:
Mn+1 = AnAn-1Mn-1
(3) Since n is an integer greater than 0, we can keep on doing this until eventually we get:
Mn+1 = AnAn-1...A1A0
NOTE:
(a) p-1 = p1 - p0a1 = a0a1 + 1 - a0a1 = 1.
(b) q-1 = 0 (see Lemma 3 above)
(c)
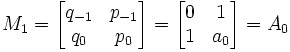
QED
Lemma 6: Mn-1 is a 2 x 2 matrix of integers.
Mn-1 =
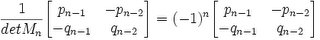
NOTE: det(Mn) = (-1)n from Lemma 4 above.
QED
Today's blog is based on H. M. Stark's An Introduction to Number Theory. If you are not familiar with Continued Fractions, start here. If you are not familiar with the Continued Fraction approximation algorithm, start here.
A continued fraction breaks a real number into a series of integers such as a0, a1, ... an. It makes sense that we can use matrices to reason about them.
In today's blog, I will focus on the simplest properties of matrices. For example, I will only deal with two types of matrices:
1 x 2 matrices such as (5,6)
2 x 2 matrices
For those who would need a review of simple matrices, matrix products, determinants, inverses, or some basic lemmas, start here.
To represent, continued fractions as matrices, we define the following:
(a) An
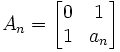
NOTE: an is taken directly from the continued fraction. See here for details on how this is generated.
(b) Mn
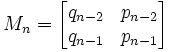
NOTE: pn, qn are generated based on the continued fraction approximation function. See here for details on how these two values are generated.
(c) γn
γn = qn-2 + αnqn-1
NOTE: αn is generated based on the continued fraction for α (see here). qn is generated based on the continued fraction approximation algorithm (see here).
Using these definitions, I will go through some lemmas that will be useful in solving Pell's equation.
Lemma 1: Mn+1 = AnMn
(1) AnMn =
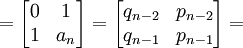
NOTE: By the definitions above.
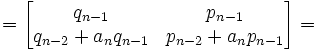
NOTE: By carrying out the matrix product [see here for review if needed]
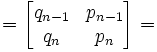
NOTE: By applying the definitions of pn and qn [see here for details]
= Mn+1 [By the definition above]
QED
Lemma 2: γn(1,α) = (1,αn)Mn
(1) (1,αn)Mn =
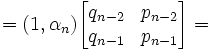
= (qn-2 + αnqn-1 , pn-2 + αnpn-1) [See here to review matrix products]
= (qn-2 + αnqn-1)(1,α) [Since α * (qn-2 + αnqn-1) = pn-2 + αnpn-1; see here]
= γn(1,α)
QED
Lemma 3: α is irrational → γn ≠ 0
(1) Since α is irrational, αn is irrational. (See here for proof; only rational numbers give way to rational αn)
(2) Assume γn = 0.
(3) Then, qn-2 + αnqn-1 = 0.
(4) Then qn-2=0 and qn-1 = 0. [See here for proof]
(5) q-1 = q1 - q0a1 = a1 - a1(1) = 0
q-2 = q0 - q-1a0 = 1 - 0*a0 = 1
NOTE: See here for review of qn
(6) We also know for all values n ≥ 1, that qn ≥ 1 (see here).
(7) So (#4) is impossible and we reject our assumption.
QED
Lemma 4: det(Mn) = (-1)n
(1) det(Mn) = pn-1qn-2 - pn-2qn-1 (See here for a review of determinants)
(2) So, det(Mn) = (-1)n by a previous result. (See here)
QED
Lemma 5: Mn+1 = AnAn-1...A1A0
(1) Mn+1 = AnMn (From Lemma 1 above)
(2) Applying Lemma 1 again gives us:
Mn+1 = AnAn-1Mn-1
(3) Since n is an integer greater than 0, we can keep on doing this until eventually we get:
Mn+1 = AnAn-1...A1A0
NOTE:
(a) p-1 = p1 - p0a1 = a0a1 + 1 - a0a1 = 1.
(b) q-1 = 0 (see Lemma 3 above)
(c)
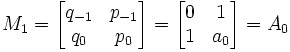
QED
Lemma 6: Mn-1 is a 2 x 2 matrix of integers.
Mn-1 =
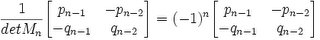
NOTE: det(Mn) = (-1)n from Lemma 4 above.
QED
Friday, December 02, 2005
Pell's Equation: The Solution
Today's blog provides the solution to Pell's Equation. For background on the history behind Pell's Equation, start here. For those not familiar with Continued Fractions, start here. I will also be using Matrices (for a review of matrix math, see here.) For a review of how matrices can be used to represent continued fractions, see here.
Pell's Equation is presented within the context of solving Fermat's Last Theorem: n=5. For those interested in the history of Fermat's Last Theorem: n=5, start here. For those interested in the proof itself, start here.
Today's blog is again based on Harold M. Stark's An Introduction to Number Theory.
Method for Solving Pell's Equation of the form: x2 - dy2 = 1 where x,y are integers.
(1) Use Continued Fractions to identify the the period for the quadratic integer √d (see here for details on the method for doing this). We will need to know at what point the period starts and its length.
For example, let's look at √3
√3 = [ 1, 1, 2 ]
The period starts at n=1 and it has a length of 2.
(2) Use Matrix Theory and Continued Fractions to find Mn-1 (see here for more details)
In the case of √3:
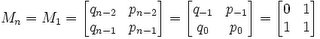

(3) Use Matrix Theory and Continued Fractions to find Mkn+p
where k is any positive integer. For the example, I will use k = 1.
In the case of √3 (see here for details on how qn and pn are defined):
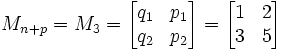
(4) Now, to find the solution, get the product of Mn-1 with Mn+p.
In the case of √3 (see here for a review of matrix products):
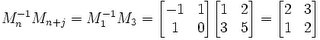
(5) Then, we find the answer in the result where x,y are found here:
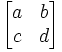
x = a
y = c
In this case of √3 :
x=2, y=1
And we see that:
(2)2 - 3(1)2 = 4 - 3 = 1
NOTE: Setting a=2, 3, 4 etc. gives us:
a=2: x=7, y = 4
a=3: x=26, y = 15
a=4: x=97, y=56
QED
Finally, here is a lemma about this method:
Lemma 1: The above method solves Pell's Equation (Sufficiency)
In other words:
(a) We let rk, sk, tk, uk be the result of Mn-1Mn+kj:
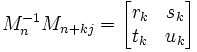
(b) We define Mn based on the Continued Fraction Approximation Algorithm so that:

(c) We further assume that:
n = the start of the period for √d and j is the length of the period such that:
√d = [ a0, a1, ... an-1, αn ]
and
αn = [ a0, ... aj-1, αn ]
(d) k is any positive integer.
Then
rk2 - dtk2 = (-1)n
Proof:
(1) Let γn = αnqn-1 + qn-2. [See here for definition of αn and qn ]
(2) We know that γn ≠ 0. [See here for proof]
(3) Let λ = γn+j/γn. [We can do this since γn ≠ 0]
(4) We note that δ(1,√d) = (1,√d)Mn-1Mn+kj
[See here for proof]
(5) From this, we can know that:
(dtk - sk) + (rk - uk)√d = 0. [See here for proof ]
(6) From a basic property of irrational numbers (see here), we know that:
dtk - sk = 0
rk - uk = 0
Therefore, we have:
uk = rk
sk = dtk
(7) Appyling this to (a) above gives us:

(8) From this, we know that:

(9) Now using the fundamentals of determinants (see here) and some lemmas found here, we know that:
det (Mn-1Mn+kj) = det(Mn-1)det(Mn+kj) =
det (Mn)-1det (Mn+kj)=
[(-1)n]-1(-1)n+kj =
(-1)-n(-1)n+kj = (-1)kj
(10) Likewise, we know that:
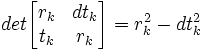
(11) So putting this together, we have show that:
rk2 - dtk2 = (-1)kj
QED
Corollary 1.1: There are either an infinite number of solutions to Pell's equation or no solutions. (Existence).
(1) We know that:
det(Mn-1Mn+kj) = (-1)kj [From Lemma 1]
(2) There are infinitely many values of k involves since k is any positive integer.
(3) When j is even, (-1)kj = 1 for all k.
(4) If j is odd, (-1)kj = 1 for all even k and (-1)kj = -1 for all odd k.
(5) Different values of k give different pairs of numbers rk and tk
(a) Suppose rk = rm, tk = tm
(b) Mn-1Mn+kj = Mn-1Mn+mj
(c) Mn+kj = Mn(Mn-1Mn+kj) = Mb(Mn-1Mn+mj) = Mn+mj
(d) Thus n+kj = n + mj and k = m (see here for proof)
(e) Therefore, k ≠ m → rk ≠ rm or tk ≠ tm
QED
Pell's Equation is presented within the context of solving Fermat's Last Theorem: n=5. For those interested in the history of Fermat's Last Theorem: n=5, start here. For those interested in the proof itself, start here.
Today's blog is again based on Harold M. Stark's An Introduction to Number Theory.
Method for Solving Pell's Equation of the form: x2 - dy2 = 1 where x,y are integers.
(1) Use Continued Fractions to identify the the period for the quadratic integer √d (see here for details on the method for doing this). We will need to know at what point the period starts and its length.
For example, let's look at √3
√3 = [ 1, 1, 2 ]
The period starts at n=1 and it has a length of 2.
(2) Use Matrix Theory and Continued Fractions to find Mn-1 (see here for more details)
In the case of √3:
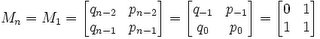

(3) Use Matrix Theory and Continued Fractions to find Mkn+p
where k is any positive integer. For the example, I will use k = 1.
In the case of √3 (see here for details on how qn and pn are defined):
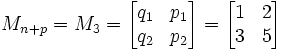
(4) Now, to find the solution, get the product of Mn-1 with Mn+p.
In the case of √3 (see here for a review of matrix products):
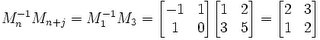
(5) Then, we find the answer in the result where x,y are found here:
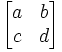
x = a
y = c
In this case of √3 :
x=2, y=1
And we see that:
(2)2 - 3(1)2 = 4 - 3 = 1
NOTE: Setting a=2, 3, 4 etc. gives us:
a=2: x=7, y = 4
a=3: x=26, y = 15
a=4: x=97, y=56
QED
Finally, here is a lemma about this method:
Lemma 1: The above method solves Pell's Equation (Sufficiency)
In other words:
(a) We let rk, sk, tk, uk be the result of Mn-1Mn+kj:
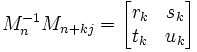
(b) We define Mn based on the Continued Fraction Approximation Algorithm so that:

(c) We further assume that:
n = the start of the period for √d and j is the length of the period such that:
√d = [ a0, a1, ... an-1, αn ]
and
αn = [ a0, ... aj-1, αn ]
(d) k is any positive integer.
Then
rk2 - dtk2 = (-1)n
Proof:
(1) Let γn = αnqn-1 + qn-2. [See here for definition of αn and qn ]
(2) We know that γn ≠ 0. [See here for proof]
(3) Let λ = γn+j/γn. [We can do this since γn ≠ 0]
(4) We note that δ(1,√d) = (1,√d)Mn-1Mn+kj
[See here for proof]
(5) From this, we can know that:
(dtk - sk) + (rk - uk)√d = 0. [See here for proof ]
(6) From a basic property of irrational numbers (see here), we know that:
dtk - sk = 0
rk - uk = 0
Therefore, we have:
uk = rk
sk = dtk
(7) Appyling this to (a) above gives us:

(8) From this, we know that:

(9) Now using the fundamentals of determinants (see here) and some lemmas found here, we know that:
det (Mn-1Mn+kj) = det(Mn-1)det(Mn+kj) =
det (Mn)-1det (Mn+kj)=
[(-1)n]-1(-1)n+kj =
(-1)-n(-1)n+kj = (-1)kj
(10) Likewise, we know that:
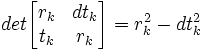
(11) So putting this together, we have show that:
rk2 - dtk2 = (-1)kj
QED
Corollary 1.1: There are either an infinite number of solutions to Pell's equation or no solutions. (Existence).
(1) We know that:
det(Mn-1Mn+kj) = (-1)kj [From Lemma 1]
(2) There are infinitely many values of k involves since k is any positive integer.
(3) When j is even, (-1)kj = 1 for all k.
(4) If j is odd, (-1)kj = 1 for all even k and (-1)kj = -1 for all odd k.
(5) Different values of k give different pairs of numbers rk and tk
(a) Suppose rk = rm, tk = tm
(b) Mn-1Mn+kj = Mn-1Mn+mj
(c) Mn+kj = Mn(Mn-1Mn+kj) = Mb(Mn-1Mn+mj) = Mn+mj
(d) Thus n+kj = n + mj and k = m (see here for proof)
(e) Therefore, k ≠ m → rk ≠ rm or tk ≠ tm
QED
Monday, November 28, 2005
Continued Fractions: Basic Properties
Today's blog is a continuation of the discussion about the famous math problem known as Pell's Equation.
In today's blog, I will show proofs for two properties of Continued Fractions (for those not familiar with Continued Fractions, start here):
ax2 + bx + c = 0
where a,b,c are integers.
For a periodic continued fraction which a period of size j and where the period begins before i, then: ai = ai+j.
The proofs outlined in today's blog are based on work done by Harold M. Stark in his book An Introduction to Number Theory.
Theorem 1: A continued fraction is finite if and only if it is a rational number.
(1) We know that if a continued fraction is finite, then it is representable as a rational number. (See Lemma 2, here)
(2) So, all we need to prove is that a rational number is representable as a finite continued fraction.
(3) For any rational number, there are two integers, let's call them c,d0 such that the rational number is representable by a/b. [Definition of a rational number]
(4) To generate a continued fraction, we need to generate a set of integers a0 through an.
(5) Let's set a0 = floor(c/d0).
A floor is a function that returns the minium integer that is less than or equal to a certain rational value. For example, the floor of (3/4) is 0. The floor of (5/2) is 2 and the floor of (-8) is -8. Finally, the floor of (-8.1) is -9.
(6) If a0 = c/d0, then we are done and the continued fraction is [a0]. Going forward, we will assume that a0 is less than but not equal to c/d0.
(7) Subtracting the original number by the a0 results in a rational number which we can call β0:
c/d0 = a0 + β0
We note that β0 is ≥ 0 and less than 1 by our assumption in #6. When it is 0 we are done.
(8) Now, from #7, we know that d0 * β0 is an integer since:
c = d0 * a0 + d0*β0
And therefore:
d0 * β0 = c - d0*a0
Which is an integer since c is an integer and d0 is an integer and a0 is an integer.
(9) So, we know there exists an integer d1 = d0 * β0.
We also note that this integer has the following properties:
(a) d1 ≥ 0.
We know that it is not negative since we can assume d0 is positive (if both c,d0 are negative, we can assume that they are both positive. If c is positive and d0 is negative, we can assume that c is negative and d0 is positive.
(b) d1 is less than d0
We know it is less than d0 since β0 is less than 1 and since d1 = d0 * β0
(10) From #9, we note that β0 = d1/d0
(11) Now, a1 = floor(1/β0) = floor(d1/d0)
Now if this is an integer (for example, 1/(1/2) = 2), then we are done and the continued fraction is [a0,a1]. So, let's assume that we are not done.
(12) So, then, there exists rational value β1 that is equal to the difference between 1/β0 and a1 which is greater than 0 so that:
d1/d0 = a1 + β1
This is the same form as step #7 and the same principles apply. We can derive a d2 that is a positive integer less than d1 and so on.
(13) Because di is an integer that continually gets smaller, we know that eventually it will equal 0.
(14) When di = 0 we are done and so we have proven that our sequence will eventually end.
QED
Lemma 1: If a continued fraction is periodic, then it represents a quadratic number.
(1) A quadratic number is any real number that satisfies the quadratic equation:
ax2 + bx + c = 0 where a,b,c are integers.
For example, √2 is a quadratic number since it satisfies the equation (a=1,b=0,c=-2) where:
x2 - 2 = 0
(2) Let α be a real number that is represented by a periodic continued fraction that repeats a am with a period of k.
So α = [ a0, a1, ..., am-1, αm]
And
αm = [ am, am+1, ..., am+k-1, am, am+1, ...]
And
αm = [ am, am+1, ..., am+k-1, αm]
(3) So, applying Lemma 1 from a previous blog, we get:
αm = (αmpm + pm-1)/(αmqm + qm-1)
(4) And multiplying (αmqm + qm-1) to both sides gives us:
(αm)2*qm + αm*qm-1 = (αmpm + pm-1)
And:
(αm)2*qm + αm*qm-1 - αmpm - pm-1 = 0
And:
(αm)2*qm + (αm)(qm-1 - pm) - pm-1= 0
(5) Applying lemma 1 from a previous blog to the first equation in #2 gives us:
α = (αm*pm-1 + pm-2)/(αm*qm-1 + qm-2)
(6) So,
α*(αm*qm-1 + qm-2) = (αm*pm-1 + pm-2)
and
α*αm*qm-1 + α*qm-2 - αm*pm-1 - pm-2 = 0
and
αm(α*qm-1 - pm-1) = pm-2 - α*qm-2
and
αm = (pm-2 - α*qm-2)/(α*qm-1 - pm-1)
(7) Now inserting (#6) into (#4) gives us:
[ ([pm-2 - α*qm-2)/(α*qm-1 - pm-1)]2*qm +
[(pm-2 - α*qm-2)/(α*qm-1 - pm-1)](qm-1 - pm) - pm-1 = 0
And multiplying (α*qm-1 - pm-1)2 to both sides give us:
(pm-2 - α*qm-2)2*qm +
(pm-2 - α*qm-2)(α*qm-1 - pm-1)(qm-1 - pm) - (α*qm-1 - pm-1)2(pm-1) = 0
(8) And solving for all the values above gives us a quadratic equation of the form:
α2a + αb + c = 0
QED
Lemma 2: If α is a quadratic number, and [a0, a1, ... , an-1, αn] is a continued fraction representation where ai are integers and αn is a real number, then αn is also a quadratic number.
(1) Since α is a quadratic number, there exists integers a,b, and c such that:
a(α)2 + b(α) + c = 0. [Definition of a quadratic number]
(2) From Lemma 1 in a previous blog, we know that:
α = (αn * pn-1 + pn-2)/(αn* qn-1 + qn-2)
(3) Inserting (1) into (2) and then multiplying everything out and then regrouping around (αn)2, αn, and any integer gives us three values An, Bn, Cn such that:
An(αn)2 + Bn(αn) + Cn = 0.
where
An = a(pn-1)2 + bpn-1qn-1 + c(qn-1)2
Bn = 2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2
Cn = a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 = An-1
(4) By definition, this means that αn is a quadratic number.
QED
Corollary 2.1: (Bn)2 - 4AnCn = b2 - 4ac
where:
An = a(pn-1)2 + bpn-1qn-1 + c(qn-1)2
Bn = 2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2
Cn = a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 = An-1
(1) From Lemma 2 above:
(Bn)2 - 4AnCn =
= (2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2)(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) - 4*[a(pn-1)2 + bpn-1qn-1 + c(qn-1)2][a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 = An-1] =
= (2apn-1pn-2 )(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) +
(bpn-1qn-2)(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) +
(bpn-2qn-1)(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) +
(2cqn-1qn-2)(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) -
(4a(pn-1)2)[a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 ] -
(4bpn-1qn-1)[a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 ] -
(4c(qn-1)2)[a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 ]
(2) Multipyling each term, we get:
(i) (2apn-1pn-2 )(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) =
4a2(pn-1)2(pn-2)2 +
2ab(pn-1)2(pn-2)(qn-2) +
2ab(pn-1)(pn-2)2(qn-1) +
4ac(pn-1)(pn-2)(qn-1)(qn-2)
(ii) (bpn-1qn-2)(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) =
2ab(pn-1)2(pn-2)(qn-2) +
b2(pn-1)2(qn-2)2 +
b2(pn-1)(pn-2)(qn-1)(qn-2) +
2bc(pn-1)(qn-1)(qn-2)2
(iii) (bpn-2qn-1)(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) =
2ab(pn-1)(pn-2)2(qn-1) +
b2(pn-1)(pn-2)(qn-1)(qn-2) +
b2(pn-2)2(qn-1)2 +
2bc(pn-2)(qn-1)2(qn-2)
(iv) (2cqn-1qn-2)(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) =
4ac(pn-1)(pn-2)(qn-1)(qn-2) +
2bc(pn-1)(qn-1)(qn-2)2 +
2bc(pn-2)(qn-1)2(qn-2) +
4c2(qn-1)2(qn-2)2
(v) -(4a(pn-1)2)[a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 ] =
-4a2(pn-1)2(pn-2)2 + -4ab(pn-1)2(pn-2)(qn-2) + -4ac(pn-1)2(qn-2)2
(vi) -(4bpn-1qn-1)[a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 ] =
-4ab(pn-1)(pn-2)2(qn-1) +
-4b2(pn-1)(pn-2)(qn-1)(qn-2) +
-4bc(pn-1)(qn-1)(qn-2)2
(vii) -(4c(qn-1)2)[a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 ] =
-4ac(pn-2)2(qn-1)2 +
-4bc(pn-2)(qn-1)2(qn-2) +
-4c2(qn-1)2(qn-2)2
(3) We can see that many of these terms line up and cancel out:
= [ 4a2(pn-1)2(pn-2)2 - 4a2(pn-1)2(pn-2)2 ]+ { from 2.i and 2.v }
[ 2ab(pn-1)2pn-2qn-2 + 2ab(pn-1)2pn-2qn-2 - 4ab(pn-1)2pn-2qn-2 ] + { from 2.i, 2.ii, and 2.iv }
[ 2ab(pn-1)(pn-2)2(qn-1) + 2ab(pn-1)(pn-2)2(qn-1) - 4ab(pn-1)(pn-2)2(qn-1) ]+ { from 2.i, 2.iii, and 2.vi }
[ 2bcpn-1(qn-1)2qn-2 + 2bcpn-1(qn-1)2qn-2 - 4bcpn-1(qn-1)2qn-2 ] + { from 2.iii, 2.iv, and 2.vii }
[ 2bcpn-2qn-1(qn-2)2 +2bcpn-2qn-1(qn-2)2 - 4bcpn-2qn-1(qn-2)2 ] + { from 2.ii, 2.iv, and 2.vi }
( 4c2(qn-1)2(qn-2)2 - 4c2(qn-1)2(qn-2)2 ) + { from 2.iv and 2.vii }
( b2pn-1pn-2qn-1qn-2 + b2pn-1pn-2qn-1qn-2 - 4b2pn-1pn-2qn-1qn-2 ) + { from 2.ii, 2.iii, and 2.vi }
(4acpn-1pn-2qn-1qn-2 + 4acpn-1pn-2qn-1qn-2) + { from 2.i and 2.iv }
[b2(pn-1)2(qn-2)2 + b2(pn-2)2(qn-1)2 ] + { from 2.ii and 2.iii }
[-4ac(pn-2)2(qn-1)2 +-4ac(pn-1)2(qn-2)2 ] { from 2.v and 2.vii }
= -2b2pn-1pn-2qn-1qn-2 + 8acpn-1pn-2qn-1qn-2 +
b2(pn-1)2(qn-2)2 +
b2(pn-2)2(qn-1)2 +
-4ac(pn-2)2(qn-1)2 +
-4ac(pn-1)2(qn-2)2 =
= b2[(pn-1)2(qn-2)2 + (pn-2)2(qn-1)2 - 2pn-1pn-2qn-1qn-2] - 4ac[(pn-1)2(qn-2)2 + (pn-2)2(qn-1)2 - 2pn-1pn-2qn-1qn-2] =
= (b2 - 4ac)[(pn-1)2(qn-2)2 + (pn-2)2(qn-1)2 - 2pn-1pn-2qn-1qn-2] =
= (b2 - 4ac)(pn-1qn-2 - pn-2qn-1)2
(4) Applying Lemma 2 from a previous blog, we get:
(b2 - 4ac)(pn-1qn-2 - pn-2qn-1)2= (b2 - 4ac)(-1)2 =
= b2 - 4ac.
QED
Corollary 2.2: An, Bn, Cn can only span over a finite set of integers.
(1) Let λn = pnqn - α(qn)2
(2) Rearranging values gives us:
pn = λn/qn - αqn
(3) We note that absolute(λn) is less than 1 since:
(a) We know that α - pn/qn is less than 1/qn2 and greater than -1/qn2. [From Theorem 2, here]
(b) Multiplying (qn)2 to all sides give us that:
α*(qn)2 - pnqn is between -1 and 1.
(c) Multiplying -1 to all sides give us that:
pnqn - α(qn)2 is between -1 and 1.
(d) This proves that λn is between -1 and 1 or rather absolute(λn) is less than 1.
(4) Inserting #2 into the formula for An in Lemma 2 gives us:
An = a( λn-1/qn-1 + αqn-1)2 + b( λn-1/qn-1 + αqn-1)an-1 + c(qn-1)2
Working this through and rearranging values gives us:
(qn-1)2(aα2 + bα + c) + 2aαλn-1 + a(λn-1)2/(qn-1)2 + bλn-1
Since we know that aα2 + bα + c = 0 (since α is a quadratic number based on a,b,c), we get:
An = 2aαλn-1 + a(λn-1)2/(qn-1)2 + bλn-1
Since absolute(λan-1) is less than 1, this tells us that:
absolute(An) is less than 2*absolute(aα) + absolute(a) + absolute(b).
To understand the details for why this is true, there are three cases to consider:
Case I: a,b positive
In this case An is less than 2*absolute(aα) + absolute(a) + absolute(b).
Case II: a,b negative
In this case, the absolute values result in values the same as in Case I. In this case An = -absolute(An).
Case III: a,b: one is negative, one is positive
In this case, An will be greater than -absolute(An) and less than absolute(An) so, then:
absolute(An) is less than 2*absolute(aα) + absolute(a) + absolute(b)
Since Cn = An-1, we know that:
absolute(Cn) is less than 2*absolute(aα) + absolute(a) + absolute(b)
Finally, since (Bn)2 = 4AnCn + b2-4ac, we know that:
(Bn)2 ≤ 4[ 2*absolute(aα) + absolute(a) + absolute(b)]2 + absolute(b2-4ac)
(5) The important idea from all this is that there are only a finite number integers that An, Bn, and Cn can equal, that is, only those integers which make up the ranges in #4.
QED
Theorem 2: A continued fraction is periodic if and only if it represents an irrational quadratic number.
(1) In Lemma 1, it was shown that a periodic continued fraction is a quadratic irrational number.
(2) Now, I will show that all quadratic irrational numbers are representable as periodic continued fractions.
(3) Let α be a quadratic number (that is, an irrational that is a solution to a quadratic equation)
(4) We know that there are an infinite number of values ai and αi that make it up (from Theorem 1 above, otherwise it would not be irrational)
(5) But at each point, there are only a finite number of values An, Bn, Cn that describe the equation that αi solves.
(6) This means that it is inevitable that a specific combination An, Bn, Cn repeats and continues to repeat.
(7) For each specific combination of An, Bn, Cn, there are two possible real values that satisfy the equation. (This observation comes from the solution to the quadratic equation, found here)
(8) So, eventually, some αi repeats.
QED
Lemma 3: If a value is representeable by a finite continued fraction with an odd number of elements, then it is representable by an even number of elements and likewise if it is representable by an even number of elements, it can be represented by an odd number of elements.
(1) Let [a0, a1, ..., an] be a finite continued fraction of n elements.
(2) Now, if an ≥ 2, then:
[ a0, a1, ..., an] = [ a0, a1, ..., an-1,1 ]
(3) Otherwise, if an = 1, then:
[ a0, a1, an-1,1 ] = [a0, a1, ... , an-1 + 1 ]
QED
In today's blog, I will show proofs for two properties of Continued Fractions (for those not familiar with Continued Fractions, start here):
- All rational numbers can be represented as a finite continued fraction.
- All irrational numbers that are solutions to a quadratic equation are periodic (that is, they repeat the same pattern of integers over and over again after a certain point)
ax2 + bx + c = 0
where a,b,c are integers.
For a periodic continued fraction which a period of size j and where the period begins before i, then: ai = ai+j.
The proofs outlined in today's blog are based on work done by Harold M. Stark in his book An Introduction to Number Theory.
Theorem 1: A continued fraction is finite if and only if it is a rational number.
(1) We know that if a continued fraction is finite, then it is representable as a rational number. (See Lemma 2, here)
(2) So, all we need to prove is that a rational number is representable as a finite continued fraction.
(3) For any rational number, there are two integers, let's call them c,d0 such that the rational number is representable by a/b. [Definition of a rational number]
(4) To generate a continued fraction, we need to generate a set of integers a0 through an.
(5) Let's set a0 = floor(c/d0).
A floor is a function that returns the minium integer that is less than or equal to a certain rational value. For example, the floor of (3/4) is 0. The floor of (5/2) is 2 and the floor of (-8) is -8. Finally, the floor of (-8.1) is -9.
(6) If a0 = c/d0, then we are done and the continued fraction is [a0]. Going forward, we will assume that a0 is less than but not equal to c/d0.
(7) Subtracting the original number by the a0 results in a rational number which we can call β0:
c/d0 = a0 + β0
We note that β0 is ≥ 0 and less than 1 by our assumption in #6. When it is 0 we are done.
(8) Now, from #7, we know that d0 * β0 is an integer since:
c = d0 * a0 + d0*β0
And therefore:
d0 * β0 = c - d0*a0
Which is an integer since c is an integer and d0 is an integer and a0 is an integer.
(9) So, we know there exists an integer d1 = d0 * β0.
We also note that this integer has the following properties:
(a) d1 ≥ 0.
We know that it is not negative since we can assume d0 is positive (if both c,d0 are negative, we can assume that they are both positive. If c is positive and d0 is negative, we can assume that c is negative and d0 is positive.
(b) d1 is less than d0
We know it is less than d0 since β0 is less than 1 and since d1 = d0 * β0
(10) From #9, we note that β0 = d1/d0
(11) Now, a1 = floor(1/β0) = floor(d1/d0)
Now if this is an integer (for example, 1/(1/2) = 2), then we are done and the continued fraction is [a0,a1]. So, let's assume that we are not done.
(12) So, then, there exists rational value β1 that is equal to the difference between 1/β0 and a1 which is greater than 0 so that:
d1/d0 = a1 + β1
This is the same form as step #7 and the same principles apply. We can derive a d2 that is a positive integer less than d1 and so on.
(13) Because di is an integer that continually gets smaller, we know that eventually it will equal 0.
(14) When di = 0 we are done and so we have proven that our sequence will eventually end.
QED
Lemma 1: If a continued fraction is periodic, then it represents a quadratic number.
(1) A quadratic number is any real number that satisfies the quadratic equation:
ax2 + bx + c = 0 where a,b,c are integers.
For example, √2 is a quadratic number since it satisfies the equation (a=1,b=0,c=-2) where:
x2 - 2 = 0
(2) Let α be a real number that is represented by a periodic continued fraction that repeats a am with a period of k.
So α = [ a0, a1, ..., am-1, αm]
And
αm = [ am, am+1, ..., am+k-1, am, am+1, ...]
And
αm = [ am, am+1, ..., am+k-1, αm]
(3) So, applying Lemma 1 from a previous blog, we get:
αm = (αmpm + pm-1)/(αmqm + qm-1)
(4) And multiplying (αmqm + qm-1) to both sides gives us:
(αm)2*qm + αm*qm-1 = (αmpm + pm-1)
And:
(αm)2*qm + αm*qm-1 - αmpm - pm-1 = 0
And:
(αm)2*qm + (αm)(qm-1 - pm) - pm-1= 0
(5) Applying lemma 1 from a previous blog to the first equation in #2 gives us:
α = (αm*pm-1 + pm-2)/(αm*qm-1 + qm-2)
(6) So,
α*(αm*qm-1 + qm-2) = (αm*pm-1 + pm-2)
and
α*αm*qm-1 + α*qm-2 - αm*pm-1 - pm-2 = 0
and
αm(α*qm-1 - pm-1) = pm-2 - α*qm-2
and
αm = (pm-2 - α*qm-2)/(α*qm-1 - pm-1)
(7) Now inserting (#6) into (#4) gives us:
[ ([pm-2 - α*qm-2)/(α*qm-1 - pm-1)]2*qm +
[(pm-2 - α*qm-2)/(α*qm-1 - pm-1)](qm-1 - pm) - pm-1 = 0
And multiplying (α*qm-1 - pm-1)2 to both sides give us:
(pm-2 - α*qm-2)2*qm +
(pm-2 - α*qm-2)(α*qm-1 - pm-1)(qm-1 - pm) - (α*qm-1 - pm-1)2(pm-1) = 0
(8) And solving for all the values above gives us a quadratic equation of the form:
α2a + αb + c = 0
QED
Lemma 2: If α is a quadratic number, and [a0, a1, ... , an-1, αn] is a continued fraction representation where ai are integers and αn is a real number, then αn is also a quadratic number.
(1) Since α is a quadratic number, there exists integers a,b, and c such that:
a(α)2 + b(α) + c = 0. [Definition of a quadratic number]
(2) From Lemma 1 in a previous blog, we know that:
α = (αn * pn-1 + pn-2)/(αn* qn-1 + qn-2)
(3) Inserting (1) into (2) and then multiplying everything out and then regrouping around (αn)2, αn, and any integer gives us three values An, Bn, Cn such that:
An(αn)2 + Bn(αn) + Cn = 0.
where
An = a(pn-1)2 + bpn-1qn-1 + c(qn-1)2
Bn = 2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2
Cn = a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 = An-1
(4) By definition, this means that αn is a quadratic number.
QED
Corollary 2.1: (Bn)2 - 4AnCn = b2 - 4ac
where:
An = a(pn-1)2 + bpn-1qn-1 + c(qn-1)2
Bn = 2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2
Cn = a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 = An-1
(1) From Lemma 2 above:
(Bn)2 - 4AnCn =
= (2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2)(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) - 4*[a(pn-1)2 + bpn-1qn-1 + c(qn-1)2][a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 = An-1] =
= (2apn-1pn-2 )(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) +
(bpn-1qn-2)(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) +
(bpn-2qn-1)(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) +
(2cqn-1qn-2)(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) -
(4a(pn-1)2)[a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 ] -
(4bpn-1qn-1)[a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 ] -
(4c(qn-1)2)[a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 ]
(2) Multipyling each term, we get:
(i) (2apn-1pn-2 )(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) =
4a2(pn-1)2(pn-2)2 +
2ab(pn-1)2(pn-2)(qn-2) +
2ab(pn-1)(pn-2)2(qn-1) +
4ac(pn-1)(pn-2)(qn-1)(qn-2)
(ii) (bpn-1qn-2)(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) =
2ab(pn-1)2(pn-2)(qn-2) +
b2(pn-1)2(qn-2)2 +
b2(pn-1)(pn-2)(qn-1)(qn-2) +
2bc(pn-1)(qn-1)(qn-2)2
(iii) (bpn-2qn-1)(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) =
2ab(pn-1)(pn-2)2(qn-1) +
b2(pn-1)(pn-2)(qn-1)(qn-2) +
b2(pn-2)2(qn-1)2 +
2bc(pn-2)(qn-1)2(qn-2)
(iv) (2cqn-1qn-2)(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) =
4ac(pn-1)(pn-2)(qn-1)(qn-2) +
2bc(pn-1)(qn-1)(qn-2)2 +
2bc(pn-2)(qn-1)2(qn-2) +
4c2(qn-1)2(qn-2)2
(v) -(4a(pn-1)2)[a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 ] =
-4a2(pn-1)2(pn-2)2 + -4ab(pn-1)2(pn-2)(qn-2) + -4ac(pn-1)2(qn-2)2
(vi) -(4bpn-1qn-1)[a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 ] =
-4ab(pn-1)(pn-2)2(qn-1) +
-4b2(pn-1)(pn-2)(qn-1)(qn-2) +
-4bc(pn-1)(qn-1)(qn-2)2
(vii) -(4c(qn-1)2)[a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 ] =
-4ac(pn-2)2(qn-1)2 +
-4bc(pn-2)(qn-1)2(qn-2) +
-4c2(qn-1)2(qn-2)2
(3) We can see that many of these terms line up and cancel out:
= [ 4a2(pn-1)2(pn-2)2 - 4a2(pn-1)2(pn-2)2 ]+ { from 2.i and 2.v }
[ 2ab(pn-1)2pn-2qn-2 + 2ab(pn-1)2pn-2qn-2 - 4ab(pn-1)2pn-2qn-2 ] + { from 2.i, 2.ii, and 2.iv }
[ 2ab(pn-1)(pn-2)2(qn-1) + 2ab(pn-1)(pn-2)2(qn-1) - 4ab(pn-1)(pn-2)2(qn-1) ]+ { from 2.i, 2.iii, and 2.vi }
[ 2bcpn-1(qn-1)2qn-2 + 2bcpn-1(qn-1)2qn-2 - 4bcpn-1(qn-1)2qn-2 ] + { from 2.iii, 2.iv, and 2.vii }
[ 2bcpn-2qn-1(qn-2)2 +2bcpn-2qn-1(qn-2)2 - 4bcpn-2qn-1(qn-2)2 ] + { from 2.ii, 2.iv, and 2.vi }
( 4c2(qn-1)2(qn-2)2 - 4c2(qn-1)2(qn-2)2 ) + { from 2.iv and 2.vii }
( b2pn-1pn-2qn-1qn-2 + b2pn-1pn-2qn-1qn-2 - 4b2pn-1pn-2qn-1qn-2 ) + { from 2.ii, 2.iii, and 2.vi }
(4acpn-1pn-2qn-1qn-2 + 4acpn-1pn-2qn-1qn-2) + { from 2.i and 2.iv }
[b2(pn-1)2(qn-2)2 + b2(pn-2)2(qn-1)2 ] + { from 2.ii and 2.iii }
[-4ac(pn-2)2(qn-1)2 +-4ac(pn-1)2(qn-2)2 ] { from 2.v and 2.vii }
= -2b2pn-1pn-2qn-1qn-2 + 8acpn-1pn-2qn-1qn-2 +
b2(pn-1)2(qn-2)2 +
b2(pn-2)2(qn-1)2 +
-4ac(pn-2)2(qn-1)2 +
-4ac(pn-1)2(qn-2)2 =
= b2[(pn-1)2(qn-2)2 + (pn-2)2(qn-1)2 - 2pn-1pn-2qn-1qn-2] - 4ac[(pn-1)2(qn-2)2 + (pn-2)2(qn-1)2 - 2pn-1pn-2qn-1qn-2] =
= (b2 - 4ac)[(pn-1)2(qn-2)2 + (pn-2)2(qn-1)2 - 2pn-1pn-2qn-1qn-2] =
= (b2 - 4ac)(pn-1qn-2 - pn-2qn-1)2
(4) Applying Lemma 2 from a previous blog, we get:
(b2 - 4ac)(pn-1qn-2 - pn-2qn-1)2= (b2 - 4ac)(-1)2 =
= b2 - 4ac.
QED
Corollary 2.2: An, Bn, Cn can only span over a finite set of integers.
(1) Let λn = pnqn - α(qn)2
(2) Rearranging values gives us:
pn = λn/qn - αqn
(3) We note that absolute(λn) is less than 1 since:
(a) We know that α - pn/qn is less than 1/qn2 and greater than -1/qn2. [From Theorem 2, here]
(b) Multiplying (qn)2 to all sides give us that:
α*(qn)2 - pnqn is between -1 and 1.
(c) Multiplying -1 to all sides give us that:
pnqn - α(qn)2 is between -1 and 1.
(d) This proves that λn is between -1 and 1 or rather absolute(λn) is less than 1.
(4) Inserting #2 into the formula for An in Lemma 2 gives us:
An = a( λn-1/qn-1 + αqn-1)2 + b( λn-1/qn-1 + αqn-1)an-1 + c(qn-1)2
Working this through and rearranging values gives us:
(qn-1)2(aα2 + bα + c) + 2aαλn-1 + a(λn-1)2/(qn-1)2 + bλn-1
Since we know that aα2 + bα + c = 0 (since α is a quadratic number based on a,b,c), we get:
An = 2aαλn-1 + a(λn-1)2/(qn-1)2 + bλn-1
Since absolute(λan-1) is less than 1, this tells us that:
absolute(An) is less than 2*absolute(aα) + absolute(a) + absolute(b).
To understand the details for why this is true, there are three cases to consider:
Case I: a,b positive
In this case An is less than 2*absolute(aα) + absolute(a) + absolute(b).
Case II: a,b negative
In this case, the absolute values result in values the same as in Case I. In this case An = -absolute(An).
Case III: a,b: one is negative, one is positive
In this case, An will be greater than -absolute(An) and less than absolute(An) so, then:
absolute(An) is less than 2*absolute(aα) + absolute(a) + absolute(b)
Since Cn = An-1, we know that:
absolute(Cn) is less than 2*absolute(aα) + absolute(a) + absolute(b)
Finally, since (Bn)2 = 4AnCn + b2-4ac, we know that:
(Bn)2 ≤ 4[ 2*absolute(aα) + absolute(a) + absolute(b)]2 + absolute(b2-4ac)
(5) The important idea from all this is that there are only a finite number integers that An, Bn, and Cn can equal, that is, only those integers which make up the ranges in #4.
QED
Theorem 2: A continued fraction is periodic if and only if it represents an irrational quadratic number.
(1) In Lemma 1, it was shown that a periodic continued fraction is a quadratic irrational number.
(2) Now, I will show that all quadratic irrational numbers are representable as periodic continued fractions.
(3) Let α be a quadratic number (that is, an irrational that is a solution to a quadratic equation)
(4) We know that there are an infinite number of values ai and αi that make it up (from Theorem 1 above, otherwise it would not be irrational)
(5) But at each point, there are only a finite number of values An, Bn, Cn that describe the equation that αi solves.
(6) This means that it is inevitable that a specific combination An, Bn, Cn repeats and continues to repeat.
(7) For each specific combination of An, Bn, Cn, there are two possible real values that satisfy the equation. (This observation comes from the solution to the quadratic equation, found here)
(8) So, eventually, some αi repeats.
QED
Lemma 3: If a value is representeable by a finite continued fraction with an odd number of elements, then it is representable by an even number of elements and likewise if it is representable by an even number of elements, it can be represented by an odd number of elements.
(1) Let [a0, a1, ..., an] be a finite continued fraction of n elements.
(2) Now, if an ≥ 2, then:
[ a0, a1, ..., an] = [ a0, a1, ..., an-1,1 ]
(3) Otherwise, if an = 1, then:
[ a0, a1, an-1,1 ] = [a0, a1, ... , an-1 + 1 ]
QED
Subscribe to:
Posts (Atom)
