The proof for Taylor's Series depends on basic calculus.
For anyone who does not feel comfortable with the notation f(x) or the concept of a mathematical function, start here.
For anyone who does not know about derivatives or about the notation f'(x), f''(x), or fn(x), start here.
Theorem: Taylor Series
if
(a) f is a function with derivatives of all orders
(b) (lim n → inf)[f(n+1)(z)]/(n+1)!(x-a)n+1 = 0
then:
f(x) = f(a) + f'(a)(x-a) + [f''(a)/2!](x-a)2 + .... + [f(n)(a)/n!](x-a)n + ....
Proof:
(1) Let n be an arbitrary positive integer.
(2) From Taylor's Formula, we have:
f(x) = Pn(x) + Rn(x)
where:
Pn(x) = f(a) + f'(a)(x-a) + f''(a)[(x-a)2]/2! + ... + f(n)[(x-a)n]/n!
and
Rn(x) = [f(n+1)(z)]/(n+1)!(x-a)n+1
where z is between a and x.
(3) From assumption b, we see that:
lim (n → inf) Rn(x) = 0.
(4) Then it follows that:
f(x) = lim (n → inf) Pn(x) =
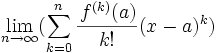
= f(a) + f'(a)(x-a) + [f''(a)/2!](x-a)2 + .... + [f(n)(a)/n!](x-a)n + ....
QED
References
- Edwards & Penny, Calculus and Analytic Geometry

No comments:
Post a Comment