The content in today's blog is taken from Harold M. Edwards Fermat's Last Theorem: A Genetic Introduction
Lemma 1:
If β is an fth root of unity and n=ef, then:
(x - yβ)*...*(x - yβn) = (xf - yf)e
Proof:
(1) Xf - 1 has f distinct roots by the Fundamental Theorem of Algebra (see here)
(2) This means that:
Xf - 1 = (X - 1)(X - β)(X - β2)*...*(X - βf-1)
(3) Since βf = 1, we have:
Xf - 1 = (X - β)(X - β2)*...*(X - βf-1)(X - βf)
(4) Let X = x/y, then we have:
(x/y)f - 1 = ([x/y] - β)([x/y] - β2)*...*([x/y] - βf)
(5) If we multiply both sides by yf, we get:
xf - yf = (x - βy)(x - β2y)*...*(x - βfy)
(6) Further, if we put both sides to the power of e, we get:
(xf - yf)e = [(x - βy)(x - β2y)*...*(x - βfy)]e =
= (x - βy)(x - β2y)*...*(x - βfy)*
(x - βf+1y)(x - βf+2)*...*(x - β2fy)*
...
(x - βf(e-1)+1)(x - βf(e-1)+2)*...*(x - βefy) =
= (x - βy)*x - β2y)*...*(βny)
QED
Theorem 2:
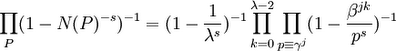
Proof:
(1) Since N(P)=pf and N(α - 1)=λ (see here for pf and here for N(α-1)=λ) and since there are e prime divisors P that divide a prime p (see here), we have:

(2) For each p, we can see that:
(1 - p-fs)-e = (1f - (p-s)f)-e
(3) Let γ be a primitive root mod λ
(4) For each p, let γj ≡ p (mod λ)
(5) Let βj be an fth root of unity such that (βj)f = 1 but for any integer i less than f, (βj)f ≠ 1.
(6) Using Lemma 1 above, we have:
(1f - (p-s)f)e = (1 - βjp-s)*...*(1 - p-sβjn) = ∏ (k=1, λ-1) (1 - βjkp-s) =
=∏ (k=0, λ-2) (1 - βjkp-s)
(7) Using step #6, we have:
(1 - λ-s)-1 ∏ (p ≠ λ) (1 - p-fs)-e = (1 - λ-s)-1 ∏ (p ≠ λ) ∏ (k=0, λ-2) (1 - p-sβjk)-1
(8) From this step, the conclusion follows:


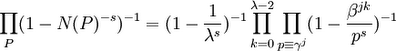
QED
References
- Harold M. Edwards, Fermat's Last Theorem: A Genetic Introduction, Springer, 2000

No comments:
Post a Comment