The content in today's blog is taken straight from Jean-Pierre Tignol's Galois Theory of Algebraic Equations. I will later use the results in today's blog in the proof by Carl Friedrich Gauss that all roots of unity are expressible as radicals.
Definition 1: μp
Let μp denote the set of p-th roots of unity.
Example:
μ1 = {1}
μ2 = {1, -1}
μ3 = {1, (1/2)[-1 + √-3], 1/2)[-1 - √-3])
μ4 = {1, -1, i, -i}
Now, let's use this to define a field (see Definition 3, here for definition of a field if needed)
Definition 2: Q(μp)
Let Q(μp) denote the set of complex numbers that are rational expressions in these p-th roots of unity.
This gives us that:

Now, we can show that Q(μp) = Q(ζ).
Lemma 1:
Q(μp) = Q(ζ)
Proof:
(1) From Defintion 1 above:
μp = { ρ1, ..., ρp}
(2) Let ζ = a primitive p-th root of unity (see Definition 2, here for definition of a primitive p-th root of unity if needed)
(3) Using Theorem 3, here, we have:
μp = { 1, ζ, ζ2, ..., ζp-1 }
(4) Then we have:

QED
Lemma 2:
Let P,Q be polynomials with coefficients in field F.
If:
P is irreducible in F[X]. (See Definition 1, here, for definition of irreducible polynomials)
P,Q have a common root u in field K which contains F
Then:
P divides Q.
Proof:
(1) Assume that P does not divide Q.
(2) Then P,Q are relatively prime polynomials since P is irreducible. [See Definition 1, here for definition of irreducible polynomials]
(3) Then (see Corollary 3.1, here), there exists polynomials U,V in F[X] such that:
P(X)U(X) + Q(X)V(X) = 1
(4) Substituting the common root u into the polynomials, we get:
P(u)U(u) + Q(u)V(u) = 1 in K
(5) Since u is the root for P(X) and Q(X), this gives us that:
P(u) = 0, Q(u) = 0 in K
(6) But then:
o*U(u) + 0*V(u) = 1 in K which is impossible.
(7) Therefore we reject our assumption in step #1.
QED
Lemma 3:
If u ∈ field K is a root of an irreducible polynomial P ∈ F[X] of degree d
and
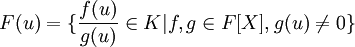
Then:
every element in F(u) can be uniquely written in the form:
a0 + a1u + a2u2 + ... + ad-1ud-1 with ai ∈ field F.
Proof:
(1) Let f(u)/g(u) be an arbitrary element in F(u)
(2) Since g(u) ≠ 0, it follows that g(u) is not divisible by P since:
(a) Assume that g(u) is divisible by P.
(b) Since P(u) = 0, if follows that (X - u) divides P. [See Theorem, here]
(c) But if P divides g(u), then (X -u) divides g(u).
(d) But this is impossible since this implies g(u) = 0 [See Theorem, here] but g(u) ≠ 0.
(e) So we reject the assumption in step #2a.
(3) Then, g(u) is relatively prime to P since P is irreducible. [See Definition 1, here for definition of irreducible polynomials]
(4) Then (see Corollary 3.1, here), there exists polynomials h,U in F such that:
g(X)h(X) + P(X)U(X) = 1 in F[X]
(5) Since P(u) = 0, substituting u for X gives us:
g(u)h(u) + P(u)U(u) = g(u)h(u) + 0*U(u) = g(u)h(u) = 1 in K.
(6) Since g(u) ≠ 0, we have:
h(u) = 1/g(u) in K
which gives us that:
f(u)/g(u) = f(u)h(u) in K
(7) Using the Division Algorithm for Polynomials (see Theorem, here), there exists Q, R such that:
fh = PQ + R in F[X] with deg R ≤ d - 1.
(8) Since P(u) = 0, it follows that:
f(u)h(u) = P(u)Q(u) + R(u) = 0*Q(u) + R(u) = R(u) in K
(9) Since R(u) is a polynomial of degree at most d-1, we have converted an arbitrary expression f(u)/g(u) ∈ F(u) into a polynomial expression of the type:
a0 + a1u + ... + ad-1ud-1
with ai ∈ F
(10) Now, I will prove uniqueness.
(11) Assume that:
a0 + a1u + ... + ad-1ud-1 = b0 + b1u + ... + bd-1ud-1
(12) Let us define V(X) such that:
V(X) = (a0 - b0) + (a1 - b1)X + ... + (ad-1 - bd-1)Xd-1 ∈ F[X]
(13) It is clear that V(u) = 0 from step #11.
(14) Using Lemma 2 above, it is clear that P divides V.
(15) But since deg V ≤ d-1 and since P is of degree d, this is impossible unless V=0.
(16) Therefore, it follows that:
a0 - b0 = a1 - b1 = ... = ad-1 - bd-1 = 0
QED
Theorem 4: Every element in Q(μp) can be expressed in one and only one way as a linear combination with rational coefficients of the p-th roots of unity other than 1:
a1ζ + a2ζ2 + ... + ap-1ζp-1
with ai ∈ Q.
Proof:
(1) Let ζ be a root of Φp [See Definition 1, here]
(2) Q(μp) = Q(ζ) [From Lemma 1 above]
(3) Since p is a prime, Φp is irreducible over Q . [See Corollary 1.1., here]
(4) Using Lemma 3 above, since the degree of ζ is p-1, it follows that every element a ∈ Q(μp) can be uniquely expressed in the form:
a = a0 + a1ζ + a2ζ2 + ... + ap-2ζp-2
for some ai ∈ Q.
(5) Using the cyclotomic equation (see Lemma 1, here), we have:
Φp(ζ) = 1 + ζ + ζ2 + ... + ζp-1 = 0
which means that:
ζ + ζ2 + ... + ζp-1 = -1
(6) This gives us that:
a0 = -a0(ζ + ζ2 + ... + ζp-1)
(7) Combining step #6 with step #4 gives us:
a = (a1 - a0)ζ + (a2 - a0)ζ2 + ... + (ap-2 - a0)ζp-2 + (-a0)ζp-1
(8) To prove uniqueness, let's assume that:
a1ζ + ... + ap-1ζp-1 = b1ζ + ... + bp-1ζp-1
(9) From step #5, we also have:
ζp-1 = -1 - ζ - ζ2 + ... -ζp-2
(10) Putting this into step #8 gives us:
a1ζ + ... + ap-1(-1 - ζ - ζ2 + ... -ζp-2) = b1ζ + ... + bp-1(-1 - ζ - ζ2 + ... -ζp-2)
which reduces to:
-ap-1 + (a1 - ap-1)ζ + (a2 - ap-1)ζ2 + ... + (ap-2 - ap-1)ζp-2 = -bp-1 + (b1 - bp-1)ζ + (b2 - bp-1)ζ2 + ... + (bp-2 - bp-1)ζp-2
(11) From Lemma 3 above, we can conclude that the coefficients on both sides are equal which gives us:
ap-1 = bp-1
which then gives us:
a1 = b1
...
ap-2 = bp-2
QED
References
- Jean-Pierre Tignol, Galois' Theory of Algebraic Equations
, World Scientific, 2001

1 comment:
Nice blog and I am here to discuss about a simple topic in mathematics that is rational expression,Rational expressions is known as an expression that is the ratio of two polynomials.It is called as rational because one number is divided by the other that is like a ratio.
Post a Comment