
where m is a prime number and R, p2, ..., pm-1 are all functions of this same form finitely nested and are functions of the coefficients of the general quintic equation.
Today's content is taken from Peter Pesic's Abel's Proof
Lemma 1:
If a mathematical expression is expressible by radicals, then it is stateable in the form:
(A1 + A2 + ... + Am)/(B1 + B2 + ... + Bn) where each Ai, Bi are expressible by radicals.
Proof:
(1) First, I show that if a mathematical expression is minimally expressible by radicals, then it is expressible by the desired form:
a + b = (a + b)/(1)
a - b = (a - b)/(1)
a * b = (a*b)/(1)
a/b = (a)/(b)
√a = (a(1/2))/(1)
(2) By the above analysis, we know that it works to at least the minimum number of operations. Let's assume that it works only up to n operations.
(3) To complete the proof, I will show that I can add an additional operation to the above form and maintain the above form. I only need to show that this is true for addition, subtraction, multiplication, division, and radicals:
(±)a + (A1 + ... + Am)/(B1 + ... + Bn) =
= (A1 + ... + Am + (±)a[B1 + ... + Bn])/(B1 + ... + Bn)
a*(A1 + ... + Am)/(B1 + ... + Bn) =
= (a*A1 + ... + a*Am)/(B1 + ... + Bn)
(1/a)*(A1 + ... + Am)/(B1 + ... + Bn) =
= (A1 + ... + Am)/(a*B1 + ... + a*Bn)
[ (A1 + ... + Am)/(B1 + ... + Bn)](1/a) = [(A1 + ... + Am)](1/a)/[(B1 + ... + Bn)(1/a)]
QED
Lemma 2:
If the general quintic equation has a solution which has the form:
y = (A1)(c1/d1) + (A2)(c2/d2) + ... + (An)(cn/dn)
where each Ai is expressible by radicals
then it can be put into the following form:
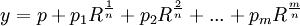
where R, p1, ..., pm-1 are all functions of this same form finitely nested.
Proof:
(1) By assumption, we can state the solution to the general quintic equation in the following form:
y = (A1)(c1/d1) + (A2)(c2/d2) + ... + (An)(cn/dn)
where each Ai are expressible as radicals.
(2) Now, if we set each A'i to (Aici), then we get:
y = (A'1)(1/d1) + (A'2)(1/d2) + ... + (A'n)(1/dn)
(3) Since, the expression has finite complexity, it follows that there can only be a finite number of expressions of the form (A'i)(1/di)
(4) So, there exists a number k such that:
[number of radicals in y] = k.
(5) Now, we can put this expression in the desired form by setting:
R = A'1
m = d1
p1 = 1
p = (A'2)(1/d2) + ... + (A'n)(1/dn)
pi = 0 where i ≠ 1.
(6) This changes y into
y = p + p1R(1/m)
(7) Now, it is clear that:
[number of radicals in p] + [number of radicals in R] = [number of radicals in y] - 1 = k-1
(8) And since we do the same refactoring for all in radicals in p and all radicals in R and since there are only a finite amount of them, we can put all radicals into the desired form.
(9) To complete the proof, we need only show that an equation without radicals can also be put into this form.
(10) So assume y does not have radicals. That is:
[number of radicals in y] = 0
(13) Then let:
p = A1c1 + A2c2 + ... + Ancn
with each pi=0.
QED
Corollary 2.1:
If the general quintic equation has a solution, then it can be put into the following form:
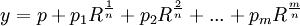
where R, p1, ..., pm-1 are all functions of this same form finitely nested.
Proof:
(1) Using Lemma 1 above, if the solution to the general equation is expressible by radicals, then it follows that y is expressible as:
y = (A1 + A2 + ... + Am)/(B1 + B2 + ... + Bn) where each Ai, Bi are expressible by radicals.
(2) Let:
T = A1 + A2 + ... + Am
W = B1 + B2 + ... + Bn
such that we have:
y = T/W
(3) Using Lemma 2 above, we know that T,W can be put in the following forms:


(4) Let:
W(x) = w0 + w1x + w2x2 + ... + wvxv
α = an n-th root of unity. (that is, α ≠ 1 and αn=1)
(5) So, we now define W0, W1, ..., Wn-1 with:
W0 = W(R(1/n)) = W
W1 = W(αR(1/n))
W2 = W(α2R(1/n))
...
Wn-1 = W(αn-1R(1/n))
(6) So, if we multiply (W1*...*Wn-1)/(W1*...*Wn-1), we get:
Y = (T*W1*...*Wv-1)/(W*W1*...*Wv-1)
(7) Multiplying W*W1*...*Wn-1 out, we get:
W*W1*W2*...*Wn-1 =
= (w0 + w1R(1/n) + w2R(2/n) + ... + wvR(v/n))*(w0 + αw1R(1/n) + α2w2R(2/n) + ... + αvwvR(v/n))*(w0 + α2w1R(1/n) + α4w2R(2/n) + ... + α2vwvR(v/n))*...*(w0 + α(n-1)w1R(1/n) + α2(n-1)w2R(2/n) + ... + αv(n-1)wvR(v/n)) =
=w0n + αw0n-1w1(1 + α + α2 + ... + αn-1) + ... α2w0n-2w2R(2/n)(1 + α + α2 + ... + αn-1) + ...
(8) Now, since (1 + α + α2 + ... + αn-1) = 0 [See Lemma 2, here], we have:
W*W1*W2*...*Wn-1 = v0n
(9) If w0n contains radicals, then we set W=w0n and we repeat the process.
(10) Since the original W has only a finite nesting of radicals, it follows that eventually we will reach a w0n that does not contain any radicals and we set each of the resulting ti = ti/(w0n)
QED
Lemma 3:
For the following expression
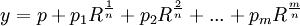
We can assume that m is less than n.
Proof:
(1) Assume that m is not less than n.
(2) Then, we there exists q,r such that (see Theorem 1, here):
m = qn + r
where q ≥ 1, and 0 ≤ r ≤ n-1
(3) Then:
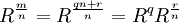
(4) Now, if we define p'i so that:
p'i = pi*Rq, then we are left with:
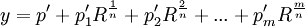
where m is less than n.
QED
Lemma 4:
For any equation of the following form:
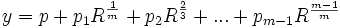
We can assume that m is prime.
Proof:
(1) Assume that m is not prime.
(2) Then m consists of a finite number of primes. [See Theorem 3, here for proof of the Fundamental Theorem of Arithmetic]
(3) Let's take out the first prime which I will call f. So that we have m = f*m'.
(4) So we can restate y as:
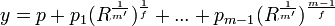
(5) Now, we can redefine each R such that:
R = R(1/m')
(6) After this, we are left with an equation of the desired form.
QED
Theorem 5: Abel's General Form
If a general solution to the quintic exists, it can be assumed to have the following form:

where m is a prime number and R, p1, ..., pm-1 are all functions of this same form finitely nested and are functions of the coefficients of the general quintic equation.
Proof:
(1) By Corollary 2.1 above:
If the general quintic equation has a solution, then it can be put into the following form:
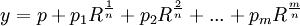
where R, p1, ..., pm-1 are all functions of this same form finitely nested.
(2) By Lemma 3 above, we can assume that m is less than n.
(3) By Lemma 4 above, we can assume that n is prime.
(4) Let R' = R/[p1n]
(5) Then we have:
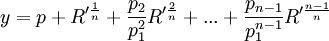
(6) Now, for all this nesting of equations of this form, at the end, each R' must be in a function of the coefficients of the general quintic equation.
(7) If not, then it does not represent a solution to the general quintic since a solution consists of determining each of the roots based on the coefficients given.
QED
References
- Peter Pesic, Abel's Proof: An Essay on the Sources and Meaning of Mathematical Unsolvability, Appendix B, The MIT Press, 2004.

6 comments:
This post seems to follow appendix B of Pesic's book. When Pesic introduces [B3] he says that it is "a function or order k, where R,q0,q1,... are functions that are of order k-1". You do not seem to mention this at all so I wonder if this turns out to be important or not later on. This assertion does not seem to have been proven. would it not be possible for qi to have be of order k and for R to be of order k-1 and the final expression [B3] to be of order k?
Hi David,
Thanks very much for your observation. This proof is based on my notes from the appendix so there is every chance that I missed that important observation.
When I have time, I'll review the appendix and modify this blog post appropriately.
Cheers,
-Larry
In Lemma 2 you show that y can be put in the form p + p1*R^(1/m) yet you only claim that it can be put in the form p + p1*R^(1/m) + p2*R^(2/m) + .... p_m_minus_1*R^((m-1)/m). Why not claim the simpler form and then use it as you move forward. Instead of carrying around the expression with m terms in it why not carry around the expression with just 2 terms in it? Can you get where you want to go with just the 2 term expression? It's so much simpler.
This might just be a minor typo but in your statement of the general form right at the beginning you say "m is a prime number and R,p2,...,pm-1 are all functions of this same form". But you make no mention of p.
Because of some of the inconsistencies that I have found with this section on Abel's form of the general solution by radicals I have gone back to Abel's 1826 paper where he presents his arguments in his own words. This is now available at
http://abel1826.blogspot.com/
In Lemma 2, point (7), it says "(7) Now, it is clear that:
[number of radicals in p] + [number of radicals in R] = [number of radicals in y] - 1 = k-1"
Could you explain this to me why the number of radicals is reduced by 1? I don't understand.
Post a Comment