Pell's Equation is presented within the context of solving Fermat's Last Theorem: n=5. For those interested in the history of Fermat's Last Theorem: n=5, start here. For those interested in the proof itself, start here.
Today's blog is again based on Harold M. Stark's An Introduction to Number Theory.
Method for Solving Pell's Equation of the form: x2 - dy2 = 1 where x,y are integers.
(1) Use Continued Fractions to identify the the period for the quadratic integer √d (see here for details on the method for doing this). We will need to know at what point the period starts and its length.
For example, let's look at √3
√3 = [ 1, 1, 2 ]
The period starts at n=1 and it has a length of 2.
(2) Use Matrix Theory and Continued Fractions to find Mn-1 (see here for more details)
In the case of √3:
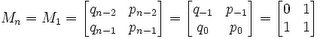

(3) Use Matrix Theory and Continued Fractions to find Mkn+p
where k is any positive integer. For the example, I will use k = 1.
In the case of √3 (see here for details on how qn and pn are defined):
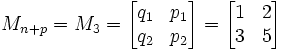
(4) Now, to find the solution, get the product of Mn-1 with Mn+p.
In the case of √3 (see here for a review of matrix products):
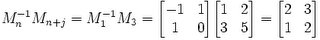
(5) Then, we find the answer in the result where x,y are found here:
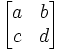
x = a
y = c
In this case of √3 :
x=2, y=1
And we see that:
(2)2 - 3(1)2 = 4 - 3 = 1
NOTE: Setting a=2, 3, 4 etc. gives us:
a=2: x=7, y = 4
a=3: x=26, y = 15
a=4: x=97, y=56
QED
Finally, here is a lemma about this method:
Lemma 1: The above method solves Pell's Equation (Sufficiency)
In other words:
(a) We let rk, sk, tk, uk be the result of Mn-1Mn+kj:
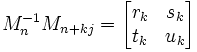
(b) We define Mn based on the Continued Fraction Approximation Algorithm so that:

(c) We further assume that:
n = the start of the period for √d and j is the length of the period such that:
√d = [ a0, a1, ... an-1, αn ]
and
αn = [ a0, ... aj-1, αn ]
(d) k is any positive integer.
Then
rk2 - dtk2 = (-1)n
Proof:
(1) Let γn = αnqn-1 + qn-2. [See here for definition of αn and qn ]
(2) We know that γn ≠ 0. [See here for proof]
(3) Let λ = γn+j/γn. [We can do this since γn ≠ 0]
(4) We note that δ(1,√d) = (1,√d)Mn-1Mn+kj
[See here for proof]
(5) From this, we can know that:
(dtk - sk) + (rk - uk)√d = 0. [See here for proof ]
(6) From a basic property of irrational numbers (see here), we know that:
dtk - sk = 0
rk - uk = 0
Therefore, we have:
uk = rk
sk = dtk
(7) Appyling this to (a) above gives us:

(8) From this, we know that:

(9) Now using the fundamentals of determinants (see here) and some lemmas found here, we know that:
det (Mn-1Mn+kj) = det(Mn-1)det(Mn+kj) =
det (Mn)-1det (Mn+kj)=
[(-1)n]-1(-1)n+kj =
(-1)-n(-1)n+kj = (-1)kj
(10) Likewise, we know that:
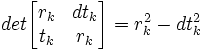
(11) So putting this together, we have show that:
rk2 - dtk2 = (-1)kj
QED
Corollary 1.1: There are either an infinite number of solutions to Pell's equation or no solutions. (Existence).
(1) We know that:
det(Mn-1Mn+kj) = (-1)kj [From Lemma 1]
(2) There are infinitely many values of k involves since k is any positive integer.
(3) When j is even, (-1)kj = 1 for all k.
(4) If j is odd, (-1)kj = 1 for all even k and (-1)kj = -1 for all odd k.
(5) Different values of k give different pairs of numbers rk and tk
(a) Suppose rk = rm, tk = tm
(b) Mn-1Mn+kj = Mn-1Mn+mj
(c) Mn+kj = Mn(Mn-1Mn+kj) = Mb(Mn-1Mn+mj) = Mn+mj
(d) Thus n+kj = n + mj and k = m (see here for proof)
(e) Therefore, k ≠ m → rk ≠ rm or tk ≠ tm
QED

8 comments:
Thank you for this awesome site!
In the beginning of the page, there is a statement:
The period starts at n=1 and it has a length of 2.
I guess, it is from here one gets "p=2"?
Just to reiterate Mikhail's point:
In step (1):
The period starts at n=1 and it has a length of 2.
In step (3):
(Use Matrix Theory and Continued Fractions to find Mkn+p
I presume that the p in step (3) is the period length from step 1?
If so could you change step 1 to:
The period starts at n=1 and it has a length of p=2.
Thanks
Rob
In the image of step (4) the second matrix in the multiplication has subscript:
n+j
should be:
n+p
Rob
In the NOTE at the end of the solution:
Setting a=2, 3, 4 etc. gives us:
Should this a be referencing the k in step (3):
Setting k=2, 3, 4 etc. gives us:
In step (d) of Lemma 1
Should:
rk^2-dtk^2=(-1)^n
be
rk^2-dtk^2=(-1)^kj
Rob
In step (d3) of Lemma 1:
Should
λ=γn+j/γn
be
δ=γn+j/γn
to match step (d4)?
Rob
Typo in step (2) of Corollary 1.1:
There are infinitely many values of k involves since k is any positive integer.
Rob
in step (5c) of Corollary 1.1:
Mn+kj = Mn(Mn-1Mn+kj) = Mb(Mn-1Mn+mj) = Mn+mj
should be
Mn+kj = Mn(Mn-1Mn+kj) = Mn(Mn-1Mn+mj) = Mn+mj
Post a Comment