If you would like to start this proof at the beginning, start here.
Today's proof is taken from Gareth A. Jones and J. Mary Jones' Elementary Number Theory.
Definition 1: Congruence Class (mod n)
The set of all numbers that are congruent to each other modulo a value n. This congruence class is represented in brackets such as [0].
NOTE: If you are not familiar with the concept of congruence or modulo, you can review modular arithmetic here.
If we consider n = 3, then we see that:
[1] = { ... ,-2, 1, 4, 7, ... }
since:
-2 ≡ 4 ≡ 7 ≡ 1 (mod 3).
Definition 2: Unit (mod p)
A congruence class [a] is a unit mod p if there exists another congruence class [b] such that ab ≡1 (mod p).
Here are some examples:
1 is a unit mod 8
3 is a unit mod 8 since (3)(3) ≡ 1 (mod 8)
5 is a unit mod 8 since (5)(5) ≡ 1 (mod 8)
7 is a unit mod 8 since (7)(7) ≡ 1 (mod 8)
Lemma 1: Let p be an odd prime. Let P be the set { 1, 2, ... (p-1)/2 }. Let x,y be elements of P.
Then: x ≠ y → x ± y is not congruent to 0.
(1) Assume that x is less than y (otherwise, we can use the same arguments on y)
(2) Case I: x + y
3 ≤ x + y ≤ (p-1)/2 + (p-1)/2 -1 = (p-1)/2 + (p-1-2)/2 = (2p -4)/2 = p-2.
(3) Case II: x-y
-1 ≥ x-y ≥ 1 - (p-1)/2 = (2 - p + 1)/2 = (-p + 3)/2 = -(p-3)/2
(4) Case III: y-x
1 ≤ y - x ≤ (p-1)/2 - 1 = (p-1-2)/2 = (p-3)/2
QED
Lemma 2: Let p be a prime, let a be an integer such that gcd(a,p)=1. Let P be the set { 1, 2, ... (p-1)/2 }. Then:
x ∈ P, y ∈ P, ax ≡ ± ay → x=y
(1) Assume that ax ≡ ± ay (mod p) and x ≠ y.
(2) ax ± ay ≡ 0 (mod p) [See here for a review of modular arithmetic if needed]
(3) So, p divides a(x ± y)
(4) But p doesn't divide a since gcd(a,p) = 1
(5) So, p divides x ± y [By Euclid's Lemma]
(6) So, x ± y ≡ 0 (mod p)
(7) But x ± y is not congruent to 0 (mod p) from Lemma 1 above.
(8) So we have a contradiction and we reject (#1)
QED
Corollary 2.1: If p is an odd prime and P = { 1, 2, ... (p-1)/2 } and gcd(a,p)=1, then there exists εi where aP = { (ε1), (ε2)(2), ... (ε(p-1)/2)[(p-1)/2] } and each εi = +1 or -1.
(1) We know that each element of aP must be in { ±1, ±2, ... ±(p-1)/2 } since:
(a) Let b be any element of P.
(b) We know that ab must fit into one of the following congruence classes [± 1], [± 2], ... [ ±(p-1)/2 ] since ab (mod p) must be between 0 and p-1.
(c) But this means that either it is between 0 and (p-1)/2 or it is between (p-1)/2 + 1 and p - 1.
(d) If it is between 0 and (p-1)/2 then we are done.
(e) If it is between (p-1)/2 + 1 and p-1, then ab (mod p) is between -(p-1)/2 and -1 since p-1 ≡ -1 (mod p) and since [(p-1)/2 + 1] ≡ -(p-1)/2 (Consider that (p-1)/2 + 1 + (p-1)/2 = (p-1+2 +p - 1)/2 = 2p/2 = p.)
(f) But then either way ab is in { ± 1, ± 2, ... ± (p-1)/2 }
(2) We know that aP = { ±1, ±2, ... ±(p-1)/2 } since:
(a) Let's suppose we have b,c such that b,c ∈ P and b ≠ c.
(b) Then, we know that that ab is not congruent to ac from Lemma 2 since it if they were congruent then they must be the same which contradicts our assumption.
QED
Lemma 3: if p is an odd prime and a is a unit mod p, then a(p-1)/2 ≡ (∏εi) (mod p) where εi is derived from aP as in Corollary 2.1 above.
(1) We know that aP = { ± 1, ± 2, ... ±(p-1)/2 } where at each point εi = 1 or -1 [See corollary 2.1]
(2) (∏εi) ≡ [(a*1)(a*2)...(a*(p-1)/2)]/[(1)(2)...(p-1)/2] (mod p)
NOTE: We can make this assumption since multiplication in modular arithmetic is an abelian group. More details here.
(3) Now, be definition of factorial [(p-1)/2]! ≡ (1)(2)...(p-1)/2 [See here for review of factorials]
(4) Likewise (a*1)(a*2)*...*(a*[p-1]/2) ≡ a(p-1)/2[(p-1)/2]! (mod p)
(5) Combining #2 with #3 and #4 gives us:
(∏εi) ≡ a(p-1)/2[(p-1)/2]!/[(p-1)/2]! = a(p-1)/2 (mod p)
QED
Lemma 4: Gauss's Lemma for Quadratic Residues
If p is an odd prime and gcd(q,p)=1, then:
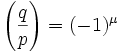
where:
μ = the number of elements in qP ∩ N
P = { 1, 2, ... (p-1)/2 }
N = { -1, -2, ... -(p-1)/2 }
(1) Let x,y be elements of P such that x ≠ y.
(2) qx is not congruent to ± qy (mod p) (from Lemma 2 above)
(3) So, we see from (2) that there are (p-1)/2 distinct congruence classes that are created from qP since for each combination, we know from (2), that there is no overlap.
(4) q(p-1)/2 ≡ (∏εi) (mod p) where εi = 1 if (i) ∈ P and εi = -1 if (i) ∈ N [From Lemma 3 above]
(5) So, q(p-1)/2 ≡ (-1)μ (mod p) where μ = the number of elements in qP ∩ N since:
(a) (∏εi) = (-1)μ where μ is the number of times εi = -1. [Since we can ignore all the times εi = 1]
(b) But this means we need to figure out the count of all elements b ∈ qP that are also in N.
(c) And this means that we are looking for the number of elements in qP ∩ N.
(6) By Euler's Criterion (see here), we know that:

(7) Combining (5) and (6) gives us our conclusion since the Legendre symbol is only = to 1 or -1.
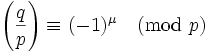
QED

1 comment:
x +/- y = 0 (mod p) is not the same as saying x = y (mod p) in Lemma 2
but Z= {1,...,n-1/2} and x and y belong to Z. x + y = v (mod p)
v will never equal 0.
Post a Comment