Quadratic reciprocity

Today's blog will focus on the following concepts: quadratic residues, Legendre symbol, and quadratic reciprocity.

The proof for the Rule of Quadratic Reciprocity can be found here.

For details on how quadratic reciprocity relates to the history of Fermat's Last Theorem, see here.

1. Quadratic Residues

The set of quadratic residues is an important concept that derives from modular arithmetic. It is the set of possible congruence values for a given value x². For example, let's look at the quadratic residues for mod 7.

There are 7 possible values for x (mod 7): 0, 1, 2, 3, 4, 5, 6 but we only need to consider the nonzero ones.

To figure out the quadratic residues, we look at the following values:

1² ≡ 1 (mod 7)
2² ≡ 4 (mod 7)
3² ≡ 9 ≡ 2 (mod 7)
4² ≡ 16 ≡ 2 (mod 7)
5² ≡ 25 ≡ 4 (mod 7)
6² ≡ 36 ≡ 1 (mod 7)

So we see that the quadratic residue for 7 consists of { 1, 2, 4}

For purposes of this blog, I will represent the quadratic residue of 7 as Q₇ so that we have:

Q₇ ≡ { 1, 2, 4 }

Since:

1² ≡ 1 (mod 5)
2² ≡ 2 (mod 5)
3² ≡ 4 (mod 5)
4² ≡ 1 (mod 5)

Q₅ ≡ { 1, 2, 4 }

2. Legendre Symbol

The Legendre Symbol is a function that can be defined in terms of quadratic residues. Consider:



This value is defined to equal 0, 1, or -1. In the case above, p is an odd prime and a is any integer. The value is 0 if p divides a. The value is 1 if a is an element of Q_p. The value is -1 if a is not an element of Q_p

We know that Q₇ ≡ { 1, 2, 4}.

If p = 7, a = 14, we know that the value of the Legendre Symbol is 0.

If p = 7, a = 15, we know that the value of the Legendre Symbol is 1 [since 15 ≡ 1 (mod 7)]

If p = 7, a = 17, we know that the value of the Legendre Symbol is -1 [ since 17 ≡ 3 (mod 7)]

3. Quadratic Reciprocity

The idea of quadratic reciprocity builds on top of the Legendre Symbol and refers to the relationship between two odd primes.

In a nutshell, the Rule of Quadratic Reciprocity states the following:



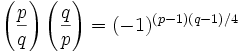
Reviewing exponents, it says that the multiple of two Legendre symbols of two primes is equal to -1 to the power of (p-1)*(q-1)/4. Since p,q are odd primes, p-1 and q-1 are even numbers and their product is divisible by 4.

There are two implications from this.

(1) If p or q ≡ 1 (mod 4), then:



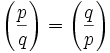
That is, p is a quadratic residue modulo q if and only if q is a quadratic residue modulo p.

This is true since:

(4k+1-1)(4k+1-1)/4 = 16k²/4=4k²=2(2k²)

(4k+1-1)(4k+3-1)/4 = (4k)(4k+2)=(16k² + 8k)/4=4k²+2k =2(2k² + k)

and

(-1)^2k' = 1.

(2) If both p and q ≡ 3 (mod 4), then:



That is, p is a quadratic residue modulo q if and only q is not a quadratic residue modulo p.

This is true since:

(4k+3-1)(4k+3-1)/4 =[16k² + 16k + 4]/4 = 4(k² + k) + 1.

and

(-1)^{4k' + 1} = -1.

This theorem is surprising and nontrivial. Carl Friedrich Gauss considered it one of the most beautiful theorems in all of number theory and worked through 7 different proofs of it. Leonhard Euler first conjectured the theory in 1783. Adrien Legendre provided several attempts at proofs. Still, it was Gauss in 1783 at the age of 18 who provided the first valid proof.