Bombelli wrote about imaginary numbers in his very influential book Algebra which was published in 1572.
Bombelli based his argument for their usefulness on Girolamo Cardano's solution for the cubic equation. Consider the following equation:
x3 = 15x + 4.
This is an example of the depressed cubic so we can use del Ferro/Tartaglia solution (see here):
b=-15
c=4
with:
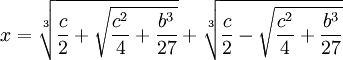
This then gives us:

So that:

which simplies to:

Cardano had considered such forms "irreducible" and had ignored them. Bombelli noticed that this wasn't quite right. For example, x3 = 15x + 4 is solved when x=4.
Bombelli proposed what he called a "wild thought". What if the term √-1 could be used mathematically so that the above value could be reduced to a number of the form: a+b√-1.
Bombelli proposed mathematical rules for allowing such numbers:
b1√-1 + b2√-1 = (b1 + b2)√-1
(b1√-1)*(b2√-1) = (-1)b1b2
and finally if:
a + bi = c + di, then a=c and b=d.
Then, using these assumptions, here's what he found:
(1) Assume that:
( a + b√-1)3 = 2 + √-121
(2) We note that (m + n)3 = m3 + n3 + 3mn(m + n) since:
(m + n)3 = m3 + 3m2n + 3mn2 + n3 = m3 + n3 + 3mn(m + n)
(3) Let m = a, n=b√-1 which gives us:
( a + b√-1)3 = a3 + b3(-1)√-1 + 3(a)(b√-1)(a + b√-1) =
=a3 - b3√-1 + 3a2(b√-1) + 3ab2(-1) =
= a(a2 -3b2) + b(3a2 - b2)√-1.
(4) Now solving for ( a + b√-1)3 = 2 + √-121 gives us:
a(a2 -3b2) = 2
b(3a2 - b2) = 11
(5) Since 2,11 are primes, we know that in both cases, one of the two factors must be 1.
If we assume that a=2,b=1, then we see that:
22 - 3(12) = 1
3*22 - 12 = 11
(6) So that:
(2 + √-1)3 = 2 + √-121.
(7) And using the same reasoning, we see that:
(2 - √-1)3 = 2 - √-121.
(8) If we assume that his reasoning is sound, we now find that:

reduces to:
x = (2 + √-1) + (2 - √-1) = 4
In this way, the theory of complex numbers was first presented by Bombelli and was eventually accepted by mathematicians.
References
- Paul J. Nahin, The Story of √-1, Princeton University Press, 1998

4 comments:
Small Typo: line 4 of step (3):
= a(a^2 -3b^2) + b(3a2 - b2)√-1.
Thanks for catching that. I just updated the entry.
-Larry
I am researching Bombelli and I have found that he did not think they assumed a+b√-1, at first he believed they formed a+√-b.
If this were the case, your explanation is invalid:
You claim that n=b√-1
but to get that from his first assumtion would be impossible as to take the b out from the radical it would be:
n=(√b)(√-1)
not just simply b.
So if we put this into the formula, it fails. Any help here?
Post a Comment