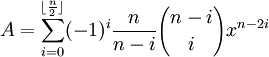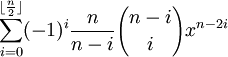Solving Van Roomen's Problem: Step Five

In today's blog, I show how we can use the trigonometric identities in my previous blog to simplify Van Roomen's x and A examples. To see the statement of Van Roomen's problem, start here.

The content in today's blog is taken from Jean-Pierre Tignol's Galois' Theory of Algebraic Equations.

Lemma 1:



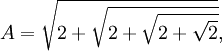
= 2 sin(15π/2⁵)

Proof:

(1) cos(90°) = 0 [See Property 7, here]

(2) cos(2π/4) = cos(π/2) = cos(90°) = 0 [See here for review of radians]

(3) 2cos(π/4) = ±√2 + 2cos(π/2) [See Lemma 1, here]

(4) So, 2cos(π/4) = ±√2

(5) 2cos(π/8) = ±√2 + 2cos(π/4) = ±√2 + √2

(6) 2cos(π/16) = ±√2 + 2cos(π/8) = ±√2 + √(2 + √2)

(7) 2cos(π/32) = ±√2 + 2cos(π/16) = ±√2 + √[2 + √(2 + √2)]

(8) 2cos(π/32) = 2sin(π/2 - π/32) [See Lemma 1, here]

(9) 2sin(π/2 - π/32) = 2sin(16π/32 - π/32) = 2sin(15π/32) = 2sin(15π/2⁵)

QED

Lemma 2:



= 2 sin(π/[2⁵*3])

Proof:

(1) 2cos(π/6) = √3 [See Corollary 1.1, here]

(2) 2cos(π/12) = ±√2 + 2cos(π/6) [See Lemma 1, here]

(3) 2cos(π/12) = ±√2 + √3

(4) 2cos(π/24) = ±√2 + 2cos(π/12) = ±√2 + √(2 + √3)

(5) 2cos(π/48) = ±√2 + 2cos(π/24) = ±√2 + √[2 + √(2 + √3)]

(5) 2sin(π/96) = ±√2 - 2cos(π/48) [See Lemma 2, here]

(6) 2sin(π/96) = 2sin(π/[2⁵*3]) = ±√2 - √{2 + √[2 + √(2 + √3)]}

QED

Lemma 3:



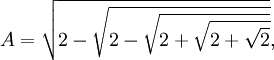
= 2 sin(15π/2⁶)

Proof:

(1) From step#6 in Lemma 1 above, we have:

2cos(π/16) = ±√2 + √(2 + √2)

(2) Using Lemma 2 here, we have:

2sin(π/32) = ±√2 - 2cos(π/16) = ±√2 - √[2 + √(2 + √2)]

(3) 2cos(π/2 - π/32) = 2sin(π/32) [See Corollary 1.1, here]

(4) 2cos(π/2 - π/32) = 2cos(16π/32 - π/32) = 2cos(15π/32)

(5) 2sin(15π/64) = ±√2 - 2cos(π/16) = ±√2 - √{2 - √[2 + √(2 + √2)]}

(6) 2sin(15π/64) = 2sin(15π/[2⁶])

QED

Lemma 4:



= 2sin(π/[2⁶*3])

Proof:

(1) Using step #5 from Lemma 2 above, we have:

2cos(π/2⁴*3) = ±√2 + 2cos(π/24) = ±√2 + √[2 + √(2 + √3)]

(2) So we have:

2cos(π/2⁵*3) = ±√2 + 2cos(π/2⁴*3) = ±√2 + √{2 + √[2 + √(2 + √3)]}

(3) And also:

2sin(π/2⁶*3) = ±√2 - 2cos(π/2⁵*3) =

= ±√2 - √(2 + √{2 + √[2 + √(2 + √3)]})

QED

Lemma 5:



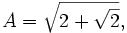
= 2sin(3π/2³)

Proof:

(1) From Lemma 1 above, step #5, we have:

2cos(π/8) = ±√2 + 2cos(π/4) = ±√2 + √2

(3) Using Lemma 1 here we have:

2cos(π/8) = 2sin(π/2 - π/8) = 2sin(4π/8 - π/8) = 2sin(3π/8) = 2sin(3π/2³)

QED

Lemma 6:



= 2sin(π/[2³*3*5])

Proof:

(1) π/5 - π/6 = 6π/30 - 5π/30 = π/30

(2) 2cos(π/30) = 2cos(π/5 - π/6) = 2cos(π/5)cos(π/6) + 2sin(π/5)sin(π/6) [See Theorem 2, here for cosine addition/subtraction rule]

(3) Using previous results, we can compute cos(π/10) and sin(π/10):

cos(π/10) = sin(π/2 - π/10) = sin(5π/10 - π/10) = sin(4π10) = sin(2π/5) [See here Lemma 1,here]

sin(2π/5) = (1/2)√(5 + √5)/2 [See Lemma 6, here]

sin(π/10) = cos(π/2 - π/10) = cos(2π/10) [See Corollary 1.1, here]

cos(2π/5) = (√5 - 1)/4 [See Lemma 5, here]

(4) Now, we can use cos(π/10), sin(π/10) to compute cos(π/5) and sin(π/5):

Using the cosine double angle formula (see Corollary 3.1, here):
cos(2x) = 2cos²(x) - 1

So,
cos(2*π/10) = cos(π/5) = 2cos²(π/10) - 1 = (2)(1/8)[5 + √5] - 1 = 5/4 + (√5)/4 - 4/4 = (√5 + 1)/4

Now, we can use sin²(π/5) + cos²(π/5) = 1 [see Corollary 2, here], to get:

sin(π/5)² = 1 - cos²(π/5) = 16/16 - (1/16)(5 + 2√5 + 1) = (1/16)[10 - 2√5 ]

This gives us:
sin(π/5) = (1/4)√10 - 2√5

(5) Using a previous result (see Corollary 1.2, here), we know that:

cos(π/6) = cos(30°) = √3/2

sin(π/6) = sin(30 °) = (1/2)

(6) So, this gives us that:

cos(π/30) = 2[(√5 + 1)/4][√3/2] + 2[(1/4)√10 - 2√5][(1/2)] =

= (1/4)[√15 + √3] + (1/4)[√10 - 2√5] =√(3/16) + √(15/16) + √(5/8) - √(5/64).

(7) 2cos(π/[2²*5*3]) = ±√2 + 2cos(π/30) [See Lemma 1, here]

So that:
2cos(π/[2²*5*3]) = ±√{2 + √(3/16) + √(15/16) + √[(5/8) - √(5/64)]}

(8) 2sin(π/[2³*5*3]) = ±√2 - 2cos(π/[2²*5*3]) [See Lemma 2, here]

So:
2sin(π/[2³*5*3]) = ±√2 - √{2 + √(3/16) + √(15/16) + √[(5/8) - √(5/64)]}

QED

Lemma 7:



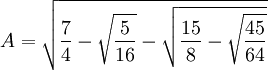
= 2 sin(π/[3*5])

Proof:

(1) 2sin(π/15) = (1/2)√7 - √5 - √(30 - 6√5) [See Corollary 7.1, here]

(2) Since (1/2) = (1/√4), we have:

2sin(π/15) = √(7/4) - √(5/16) - √[(30 - √[36*5])/16] =

= √(7/4) - √(5/16) - √[15/8 - √(36*5/16*16)] =

= √(7/4) - √(5/16) - √[15/8 - √(9*5/4*16)] =

= √(7/4) - √(5/16) - √[15/8 - √(45/64)]

QED

References

• Jean-Pierre Tignol, Galois' Theory of Algebraic Equations, World Scientific, 2001

Solving Van Roomen's Problem: Step Four

In today's blog, I will present some simple trigonometric identities that can be used to simplify Van Roomen's examples of x and A values. For those who want an introduction to Van Roomen's Problem, start here. In my next blog, I will apply these lemmas to Van Roomen's problem.

The content in today's blog is taken from Jean-Pierre Tignol's Galois' Theory of Algebraic Equations.

Let me start by introducting the some basic ideas from trigonometry.

Lemma 1: 2 cos(α/2) = ± √2 + 2 cos α

Proof:

(1) cos(2x) = 2 cos²(x) - 1 [See Corollary 3.1, here]

(2) Let x = α/2, then we get:

cos(α) = 2cos²(α/2) - 1

(3) Rearranging terms gives us:

2cos²(α/2) = cos(α) + 1

(4) Multiplying both sides by 2 gives us:

4cos²(α/2) = 2cos(α) + 2

(5) Finally, taking the square root of both sides gives us:

2cos(α/2) = ±√2 + 2cos(α)

QED

Lemma 2: 2 sin(α/2) = ± √2 - 2 cos α

Proof:

(1) cos(2x) = 1 - 2 sin²(x) [See Corollary 3.1, here]

(2) Let x = α/2, then we get:

cos(α) = 1 - 2sin²(α/2)

(3) Rearranging terms gives us:

2sin²(α/2) = 1 - cos(α)

(4) Multiplying both sides by 2 gives us:

4sin²(α/2) = 2 - 2cos(α)

(5) Finally, taking the square root of both sides gives us:

2sin(α/2) = ±√2 - 2cos(α)

QED

Lemma 3: 2 cos(π/3) = 1

Proof:

(1) 2cos(π/3) = 2cos(60°) [See here for review of radians]

(2) 2cos(60°) = 2(1/2) = 1 [See Corollary 1.2, here]

QED

Lemma 4: 2 sin(π/3) = √3

Proof:

(1) 2sin(π/3) = 2sin(60°) [See here for review of radians]

(2) 2sin(60°) = 2*(√3/2) = √3 [See Corollary 1.2, here]

QED

Lemma 5: 2cos(2π/5) = (√5 - 1)/2

Proof:

(1) cos (2π/5) = (√5 - 1)/4 [See Corollary 1.1, here]

(2) So:

2cos(2π/5) = (√5 - 1)/2

QED

Lemma 6: 2sin(2π/5) = √(5 + √5)/2

Proof:

(1) sin (2π/5) = √5 + √5/8 [See Corollary 1.1, here]

(2) So:

2*sin (2π/5) = 2(1/2)√5 + √5/2 = √(5 + √5)/2

QED

Lemma 7: 2cos(π/15) = (1/4)(√30 + 6√5 + √5 - 1)

Proof:

(1) 2π/5 - π/3 = 6π/15 - 5π/15 = π/15

(2) 2cos(π/15) = 2cos(2π/5 - π/3) = 2cos(2π/5)cos(π/3) + 2sin(2π/5)sin(π/3) [See Theorem 2, here]

2cos(2π/5) = (√5 - 1)/2 [See Lemma 5 above]

cos(π/3) = 1/2 [See Lemma 3 above]

2sin(2π/5) = √(5 + √5)/2 [See Lemma 6 above]

sin(π/3) = √3/2 [See Lemma 4 above]

(4) 2cos(π/15) = [ (√5 - 1)/2 ][1/2] + [√(5 + √5)/2][√3/2] =

= [ (√5 - 1)/4] +(1/2) [√(15 + 3√5)/2] = [ (√5 - 1)/4] + (1/4)[√(30 + 6√5)]

= (1/4)[ √5 - 1 + √(30 + 6√5)]

QED

Corollary 7.1: 2sin(π/15) = (1/2)√7 - √5 - √(30 - 6√5)

Proof:

(1) 2cos(π/15) = (1/4)(√30 + 6√5 + √5 - 1) [See Lemma 7 above]

(2) 4cos²(π/15) = (1/16)(30 + 6√5 + 5 + 1 + 2(√30 + 6√5)(√5) - 2√30 + 6√5 - 2√5 = (1/16)(36 + 4√5 + 2(√30 + 6√5)(√5) - 2√30 + 6√5)

(3) Since sin²(x) + cos²(x) = 1 [See Corollary 2, here], we have:

4sin²(π/15) = 4 - cos²(π/15) =

= (1/16)[64 - 36 - 4√5 - 2(√30 + 6√5)(√5) + 2√30 + 6√5 ] =

= (1/16)[28 - 4√5 - 2(√30 + 6√5)(√5) + 2√30 + 6√5] =

= (1/16)[28 - 4√5 - (√30 + 6√5)(2√5 - 2)] =

= (1/16)[28 - 4√5 - (√30 + 6√5)(√2√5 - 2)²] =

= (1/16)[28 - 4√5 - (√30 + 6√5)(√20 - 8√5 + 4)] =

= (1/16)[28 - 4√5 - (√30 + 6√5)(√24 - 8√5)] =

= (1/16)[28 - 4√5 - (√720 - 240√5 + 144√5 - 240)] =

= (1/16)[28 - 4√5 - (√480 - 96√5] =

= (1/16)[28 - 4√5 - 4(√30 - 6√5]


(4) 2sin(π/15) = √(1/16)[28 - 4√5 - 4(√30 -6√5] =

= (1/4)√[28 - 4√5 - 4(√30 -6√5] =

= (1/2)√[7 - √5 - √30 -6√5] =

QED

References

• Jean-Pierre Tignol, Galois' Theory of Algebraic Equations, World Scientific, 2001

Solving Van Roomen's Problem: So far

So, up to know, I've shown that Van Roomen's monster equation: (see here):

(45)x - (3,795)x³ + (95,634)x⁵ - (1,138,500)x⁷ + (7,811,375)x⁹ - (34,512,075)x¹¹ + (105,306,075)x¹³ - (232,676,280)x¹⁵ + (384,942,375)x¹⁷ - (488,494,125)x¹⁹ + (483,841,800)x²¹ - (378,658,800)x²³ + (236,030,652)x²⁵ - (117,679,100)x²⁷ + (46,955,700)x²⁹ - (14,945,040)x³¹ + (3,764,565)x³³ - (740,259)x³⁵ + (111,150)x³⁷ - (12,300)x³⁹ + (945)x⁴¹ - (45)x⁴³ + x⁴⁵ = A

simplifies to this one when n = 45 (see here for proof):



If we generalize the above equation to F_n (see below), there is an interesting recurrence relation that emerges (see here for details).

If we define:

F_n(x) =



Then:

F_n(x) = x*F_n-1(x) - F_n-2(x).

Finally, we can introduce trigonometry to the equation defined above (see here for proof) to get:

for any integer n ≥ 1:

2cos(nα) = F_n(2cosα)

For any odd integer n ≥ 1:

2 sin(nα) = (-1)^(n-1)/2*F_n(2sinα)


Now, let's see if we can simplify the examples that Van Roomen gives for x and A (see here for details). It turns out that all can be simplified using trigonometric identities.

Here are three examples that Van Roomen provides. I should note that in Van Roomen's original problem, he made a mistake on example 2. For purposes of this blog, I have corrected his mistake. (See Jean-Pierre Tignol's book for more details).

Example 1:

If



Then:



Example 2:

If:



Then:



Example 3:

If:



Then:




In my next blog, I will show how each of these values can be simplified using trigonometry.

References

• Jean-Pierre Tignol, Galois' Theory of Algebraic Equations, World Scientific, 2001

Solving Van Roomen's Problem: Step Three

The third step in solving Van Roomen's problem is realizing its relation to trigonometry. Using F_n(x) defined in my last blog (see here), I will show that:

2cos(nα) = F_n(2cosα) where n ≥ 1.

and

2sin(nα) = (-1)^(n-1)/2F_n(2sinα) where n is odd and n ≥ 1.

Here are the details:

Lemma 1: n ≥ 1 → 2 cos(n)α = (2cos α)(2 cos (n-1)α) - 2 cos(n-1)α

Proof:

(1) From the addition and subtraction cosine formulas [see Theorem 1, here], we know that:

cos (a + b) = cos a cos b + sin a sin b

cos (a - b) = cos a cos b - sin a sin b

(2) Adding these two identities together gives us:

cos (a + b) + cos (a - b) = cos a cos b + cos a cos b = 2cos a cos b

Or in other words:

cos (a + b) = 2 cos a cos b - cos (a - b)

(3) Since a,b can be any value, let b = α, let a = (n-1)α

So that:

a + b = (n-1)b + b = (n-1+1)b = nα

a - b = (n-1)b - b = (n-2)α

(4) This then gives us that:

cos (nα) = (cos α)(2 cos(n-1)α) - cos(n-2)α

Or equivalently:

2 cos (nα) = (2 cos α)(2 cos(n-1)α) - 2 cos(n-2)α

QED

This trigonometric identity is relevant to Van Roomen's problem because it fits the same structure as F_n

In my previous blog, I showed that F_n(x) = x*F_n-1(x) - F_n-2(x).

Now, if x = 2 cos α, then we have:

F_n(2 cos α) = (2 cos α)*F_n-1(2 cos α) - F_n-2(2 cos α)

This brings us to the corollary:

Corollary 1.1: 2 cos(nα) = F_n(2 cos α)

Proof:

(1) At n = 1:

F₁ = x = 2 cos α = 2 cos(n α)

(2) At n = 2:

F₂ = x² - 2 = (2 cos α)² - 2 = 2(2 cos²(α) - 1)

Since sin²(x) + cos²(x) = 1 (see Corollary 2, here), we have :

2(2 cos²(α) - 1) = 2(2 cos²(α) - [sin²(α) + cos²(α)] ) = 2[cos²(α) - sin²(α)]

Using the formula for cos(2x) (see Lemma 3, here), we get:

2[cos²(α) - sin²(α)] = 2 (cos 2 α)

(3) So, let's assume that F_n(2 cos α) = 2 cos n α up to n-1 where n ≥ 3.

(4) Now, using our previous formula (see Theorem 1, here), we know that:

F_n(x) = x*F_n-1(x) - F_n-2(x)

(5) Using our assumption in step #3, we have:

F_n(2 cos α) = (2 cos α)*(2 cos(n-1)α) - (2 cos(n-2)α)

(6) Now, using Lemma 1 above, we know that:

2 cos nα = (2 cos α)*(2 cos (n-1)α) - (2 cos(n-2)α) so that by induction (see Theorem, here for review if needed), we have proven that:

F_n(2 cos α) = 2 cos n α

QED

But we are not yet done, we can also show:

Corollary 1.2: For all odd n ≥ 1:

2 sin nα = (-1)^(n-1)/2F_n(2 sin α)

Proof:

(1) From a previous result (see Lemma 1, here), we know that:

cos(z) = sin(z + π/2) where z is any number in radians (see here for review of radians).

(2) Let z = x - π/2

(3) Then:

cos(x - π/2) = sin(x - π/2 + π2) = sin(x)

(4) Now from Corollary 1.1 above, we have:

2 cos(nα) = F_n(2 cos α)

(5) Since α can be any value let α = β - π/2

so that:

2 cos(n[β - π/2]) = 2 cos(nβ - nπ/2) = 2 cos([nβ - (n-1)π/2] - π/2) = 2 sin(nβ - (n-1)π/2)

and

F_n(2 cos (β - π/2)) = F_n(2sin(β))

(6) Using the formula for sin(a+b) [see Theorem 1, here], we get:

sin(nβ - (n-1)π/2) = sin(nβ)cos([n-1]π/2) - cos(nβ)sin([n-1]π/2)

(7) Since n is odd, we know that n-1 is even and there exists m such that (n-1)=2m which gives us:

cos([n-1]π/2) = cos(mπ) = (-1)^m since:

(a) n ≥ 1 so m ≥ 0.

(b) cos(0) = 1, cos(π)= -1 [See Property 6, here]

(c) Finally cos(x + 2π) = x [See Property 5, here]

(d) If m is even, then mπ is divisible by 2π and cos(mπ) = 1 = (-1)^m

(e) If m is odd, then mπ is not divisible by 2π and cos(mπ) = -1 = (-1)^m

Likewise:

sin([n-1]π/2) = sin(mπ) = 0 since:

(a) n ≥ 1 so m ≥ 0.

(b) sin(0) = 0, sin(π) = 0 [see Property 1, here]

(c) sin(x + 2π) = sin x [See Property 5, here]

(d) Putting this together, we can see that mπ ≡ 0 or ≡ π (mod 2π) and either way sin(mπ)=0.

(8) So that we have:

2 sin(nβ - (n-1)π/2) = 2*[sin(nβ)cos([n-1]π/2) - cos(nβ)sin([n-1]π/2)] = 2*(-1)^(n-1)/2*sin(nβ) - cos(nβ)*0 = 2*(-1)^(n-1)/2sin(nβ)

(9) Using step #8 and combining it with step #4 and step #5 gives:

2*(-1)^(n-1)/2sin(nβ) = F_n(2sin(β))

(10) Multiplying both sides by (-1)^(n-1)/2 gives us:

2sin(nβ) = (-1)^(n-1)/2F_n(2sin(β))

QED

References

• "Cos of multiples of x, in terms of cos x ", MathHelp
• Jean-Pierre Tignol, Galois' Theory of Algebraic Equations, World Scientific, 2001

Solving Van Roomen's Problem: Step Two

In my previous blog, I showed how Van Roomen's problem could be reduced to a summation formula:

(45)x - (3,795)x³ + (95,634)x⁵ - (1,138,500)x⁷ + (7,811,375)x⁹ - (34,512,075)x¹¹ + (105,306,075)x¹³ - (232,676,280)x¹⁵ + (384,942,375)x¹⁷ - (488,494,125)x¹⁹ + (483,841,800)x²¹ - (378,658,800)x²³ + (236,030,652)x²⁵ - (117,679,100)x²⁷ + (46,955,700)x²⁹ - (14,945,040)x³¹ + (3,764,565)x³³ - (740,259)x³⁵ + (111,150)x³⁷ - (12,300)x³⁹ + (945)x⁴¹ - (45)x⁴³ + x⁴⁵ =



where n = 45.

In today's blog, I will show how a recurrence relation can be introduced to simplify the problem further.

The key insight comes to generalizing the above summation formula. For example, let's define:

F_n(x) =



It turns out that it is possible to show that for any n ≥ 1:

2cos(nα) = F_n(2cosα)

For any odd n ≥ 1:

2 sin(nα) = (-1)^(n-1)/2*F_n(2sinα)

François Viète knew both of these identities and he would use them to find his solutions to Van Roomen's problem. In today's blog, I will show the proof for the recurrent relation and in my next blog, I will show how this recurrence relation leads to the trigonometric identities above.

Theorem 1: Recurrence Formula

If:

F_n(x) =



Then:

F_n(x) = x*F_n-1(x) + F_n-2(x)

Proof:

(1) F₁(x) = (-1)⁰*(1/1)*[(1!)/(0!1!)]x^1-0 = x

(2) F₂(x) = (-1)⁰*(2/2)*[(2!)/(0!2!)]x^2-0 + (-1)¹*(2/1)*[(1!)/(1!0!)]x^2-2 = x² - 2

(3) F₃(x) = (-1)⁰*(3/3)*[(3!)/(0!3!)]x^3-0 + (-1)¹*(3/2)*[(2!)/(1!1!)]x^3-2 = x³ - 3x

(4) We can see that x*F₂(x) - F₁(x) = x*(x² - 2) - x = x³ - 3x.

(5) So, we can assume that the recurrence formula is true up to some integer n-1 where n ≥ 4, that is:

F_n-1(x) = x*F_n-2(x) - F_n-3(x)

(6) Now, x*F_n-1(x) =



=


(7) Likewise, F_n-2(x) =



=



=



(8) So, we see that: x*F_n-1(x) - F_n-2(x) =





where if n is odd,

C = 0

and if n is even,

C =

-(-1)^{(n/2 - 1)}[(n-2)/(n-1-n/2)][(n-1-n/2)!/(n/2-1)!(n-1-n/2-(n/2-1))!]x^n-2(n/2) =

= (-1)^(n/2)[(n-2)/(n/2-1)][(n/2-1)!/(n/2 -1)!(0!)]x⁰ =

= (-1)^(n/2)[(n-2)]/[(n/2-1)](1)(1) = (-1)^(n/2)(n-2)*(2)/(n-2) =

= (-1)^(n/2)*2

(9) So, x*F_n-1(x) - F_n-2(x) - C - x_n =



(10) Focusing solely on the middle part, we see that:
















(11) If n is odd:

F_n(x) =



(12) If n is even:

F_n(x) =



(13) So, either way we have:

F_n(x) = x*F_n-1(x) - F_n-2(x).

QED

Solving Van Roomen's Problem: Step One

In the last blog, I presented Van Roomen's Problem:

(45)x - (3,795)x³ + (95,634)x⁵ - (1,138,500)x⁷ + (7,811,375)x⁹ - (34,512,075)x¹¹ + (105,306,075)x¹³ - (232,676,280)x¹⁵ + (384,942,375)x¹⁷ - (488,494,125)x¹⁹ + (483,841,800)x²¹ - (378,658,800)x²³ + (236,030,652)x²⁵ - (117,679,100)x²⁷ + (46,955,700)x²⁹ - (14,945,040)x³¹ + (3,764,565)x³³ - (740,259)x³⁵ + (111,150)x³⁷ - (12,300)x³⁹ + (945)x⁴¹ - (45)x⁴³ + x⁴⁵ = A

where:




Each of the coefficients is large and none of them are prime. Nineteen of them, for example, are divisible by 5. 95,634 is divisible by 7. 236,030,652 is divisible by 12. 740,259 is divisible by 3.

In addition, if we examine the coefficients in series from x¹ thru x⁴⁵, we can see that they are smallest at the edges and progressively larger toward the middle. This is a pattern also exhibited by binomials such as (x + y)ⁿ.

François Viète was able to reformulate's Adriaan van Roomen's equation into a summation equation. Using modern notation, he reduced the problem to:



where:

n = 45

= the largest integer ≤ n/2



[See here for review of factorial (!) if needed]


The floor(n/2) function is used because we only want to generate 22 different terms. Van Roomen's equation consists solely of odd powers.

If you want to see that it works, you can work it out for each term. Here are some examples of how the summation formula works:

At i=0:

(-1)⁰*(45/45)*[(45)!/(0!45!)]x⁴⁵ = x⁴⁵

At i=1:

(-1)¹*(45/44)[(44)!/(1!43!)]x⁴³ = -45x⁴³

Let's skip to i=11:

(-1)¹¹*(45/34)*[(34)!/(11!23!)]x²³ = -(45*33!)/(11!23!)x²³ = -(378,658,800)x²³

and so on up to i=22:

(-1)²²*(45/23)*[(23)!/(22!1!)]x¹ = 45x

In my next blog, I will show how a recurrence relation can further simplify the problem.

References

• Jean-Pierre Tignol, Galois' Theory of Algebraic Equations, World Scientific, 2001

Van Roomen's Problem

Adriaan Van Roomen was a professor of mathematics and medicine in Louvain who had developed a strong reputation as one of the top mathematicians of his age. In 1593, he published a survey of the most important living mathematicians. In this work, he proposed a math problem that he dared any of these top mathematicians to solve:

(45)x - (3,795)x³ + (95,634)x⁵ - (1,138,500)x⁷ + (7,811,375)x⁹ - (34,512,075)x¹¹ + (105,306,075)x¹³ - (232,676,280)x¹⁵ + (384,942,375)x¹⁷ - (488,494,125)x¹⁹ + (483,841,800)x²¹ - (378,658,800)x²³ + (236,030,652)x²⁵ - (117,679,100)x²⁷ + (46,955,700)x²⁹ - (14,945,040)x³¹ + (3,764,565)x³³ - (740,259)x³⁵ + (111,150)x³⁷ - (12,300)x³⁹ + (945)x⁴¹ - (45)x⁴³ + x⁴⁵ = A

where:



To show that Van Roomen had a solid understanding of this monstrous equation, he observed the following:

(a) If:



Then:



(b) If:



Then:



(c) If:



Then:



This problem was mentioned in a meeting between the Dutch ambassador and the King Henry IV of France. The Dutch ambassador had noted that not a single French mathematician had been listed in van Roomen's survey of the great mathematicians.

King Henry IV presented the problem to François Viète who was able to solve it. Viète's solution is historically significant because he not only demonstrated how trigonometry can be used to solve algebraic equations, he also showed that this problem possessed 45 different solutions. This result was important in helping to establish the Fundamental Theorem of Algebra.

How did Viète solve it? I will show his solution in my next blog.

References

• Eli Maor, Trigonometric Delights, Princeton Paperbacks, 1998
• Jean-Pierre Tignol, Galois' Theory of Algebraic Equations, World Scientific, 2001