Lemma 1:
Let μn be the set of all nth roots of unity
Then:

Proof:
(1) We know that xn - 1 has n root from the Fundamental Theorem of Algebra.
(2) We also note that for all ζ, we have (ζ)n = 1
(3) Based on #2, the Fundamental Theorem of Algebra gives us:
xn - 1 = (x - ζ1)*(x - ζ2)*(x - ζ3)*...*(x - ζn)
(4) Step #3 can then be restated as:

QED
Corollary 1.1:

Proof:
This follows from applying De Moivre's proof [see Corollary 1.1, here] for the existence of the roots of complex numbers with the result in Lemma 1 above.
QED
Corollary 1.2:

Proof:
This follows from applying De Moivre's proof [see Corollary 1.2, here] for the existence of the roots of complex numbers with the result in Lemma 1 above.
QED
Theorem 2:
If n is odd:

If n is even:

Proof:
(1) From Corollary 1.1 above, we have:

(2) Now, we can remove the k=0 case to get the following:

(3) Now, it is also possible to pair up roots. That is, let l = n - k.
(4) Then we have:
cos(2[(n-k)π]/n) =
=cos([2nπ - 2kπ]/n) =
=cos([2nπ/n] - [2kπ/n]) =
=cos(2π - 2kπ/n) =
cos(-2kπ/n) = cos(2kπ/n) [See Property 9, here]
sin(2[(n-k)π]/n) =
=sin([2nπ - 2kπ]/n) =
=sin([2nπ/n] - [2kπ/n]) =
=sin(2π - 2kπ/n) =
=sin(-2kπ/n) = -sin(2kπ/n) [See Property 4, here]
(5) So, pairing the roots of unity k with its n-k pair gives us:







(6) So, if n is odd, we have:

(7) If n is even, then at k=n/2 we have:
cos([2(n/2)π]/n) = cos(nπ/n) = cos(π) = -1 [See Property 6, here]
sin([2(n/2)π]/n) = sin(nπ/n) = sin(π) = 0 [See Property 1, here]
So:
[x - cos([2(n/2)π];/n) - isin([2(n/2)π]/n)] =
= x - (-1) - i*0 = x + 1
(8) So, if n is even, we have:

since we can see that n/2 is not included in any of the pairings:
k = 1 .. (n/2)-1
n-k = (n/2)+1 .. n-1
QED
Corollary 2.1:


Proof:
(1) Assume that n is odd.
(2) Then from Theorem 2 above, we have:

(3) Since n is odd, there exists m such that n = 2m+1.
(4) This then gives us:
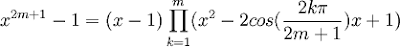
(5) Setting x = (a/x) gives us:
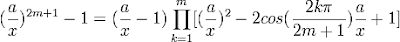
(6) Multiplying both sides by x2m+1 gives us:

(7) Assume that n is even.
(8) Then, from Theorem 2 above we have:

(9) Since n is even, there exists an integer m such that n = 2m.
(10) This then gives us:

(11) Setting x = (a/x) gives us:

(12) Multiplying both sides by x2m gives us:

QED
Theorem 3:
If n is odd:

If n is even:

Proof:
(1) From Corollary 1.2 above, we have:

(2) Now, it is also possible to pair up roots. That is, let l = n - k -1.
(3) Then we have:
cos([2(n-k-1)+1]π/n) =
=cos([2n - 2k -1]π/n) =
=cos([2nπ/n] - [(2k+1)π/n] ) =
=cos(2π - (2k+1)π/n) =
cos(-[2k+1]π/n) = cos([2k+1]π/n) [See Property 9, here]
sin([2(n-k-1)+1]π/n) =
=sin([2n - 2k - 1]π/n) =
=sin([2nπ/n] - [(2k+1)π/n]) =
=sin(2π - (2k+1)π/n) =
=sin(-[2k+1]π/n) = -sin([2k+1]π/n) [See Property 4, here]
(4) So, pairing each roots of unity k with its n-k-1 pair gives us:







(5) If n is even, the we have:

(6) If n is odd, then at k=(n-1)/2:
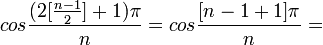

and


(7) So:

= x - (-1) - i*0 = x + 1
(8) So, if n is odd, we have:

since we can see that (n-1)/2 is not included in any of the pairings:
k = 0 .. (n-1)/2 - 1
n-k-1 = (n-1)/2 + 1 .. n-1
since:
n-[(n-1)/2 - 1] - 1 =
= n - (n-1)/2 + 1 - 1 =
= (2n - [n-1])/2 =
= (n + 1)/2 =
= (n - 1 + 2)/2 =
(n-1)/2 + 1
QED
Corollary 3.1:


Proof:
(1) Assume that n is odd.
(2) Then from Theorem 3 above, we have:

(3) Since n is odd, there exists m such that n = 2m+1.
(4) This then gives us:

(5) Setting x = (a/x) gives us:

(6) Multiplying both sides by x2m+1 gives us:

(7) Assume that n is even.
(8) Then, from Theorem 3 above we have:

(9) Since n is even, there exists an integer m such that n = 2m.
(10) This then gives us:

(11) Setting x = (a/x) gives us:

(12) Multiplying both sides by x2m gives us:

QED
References
- Jean-Pierre Tignol, Galois' Theory of Algebraic Equations
, World Scientific, 2001

No comments:
Post a Comment